นิตยสาร สสวท. ฉบับที่ 193 มีนาคม - เมษายน 2558

20 / 62

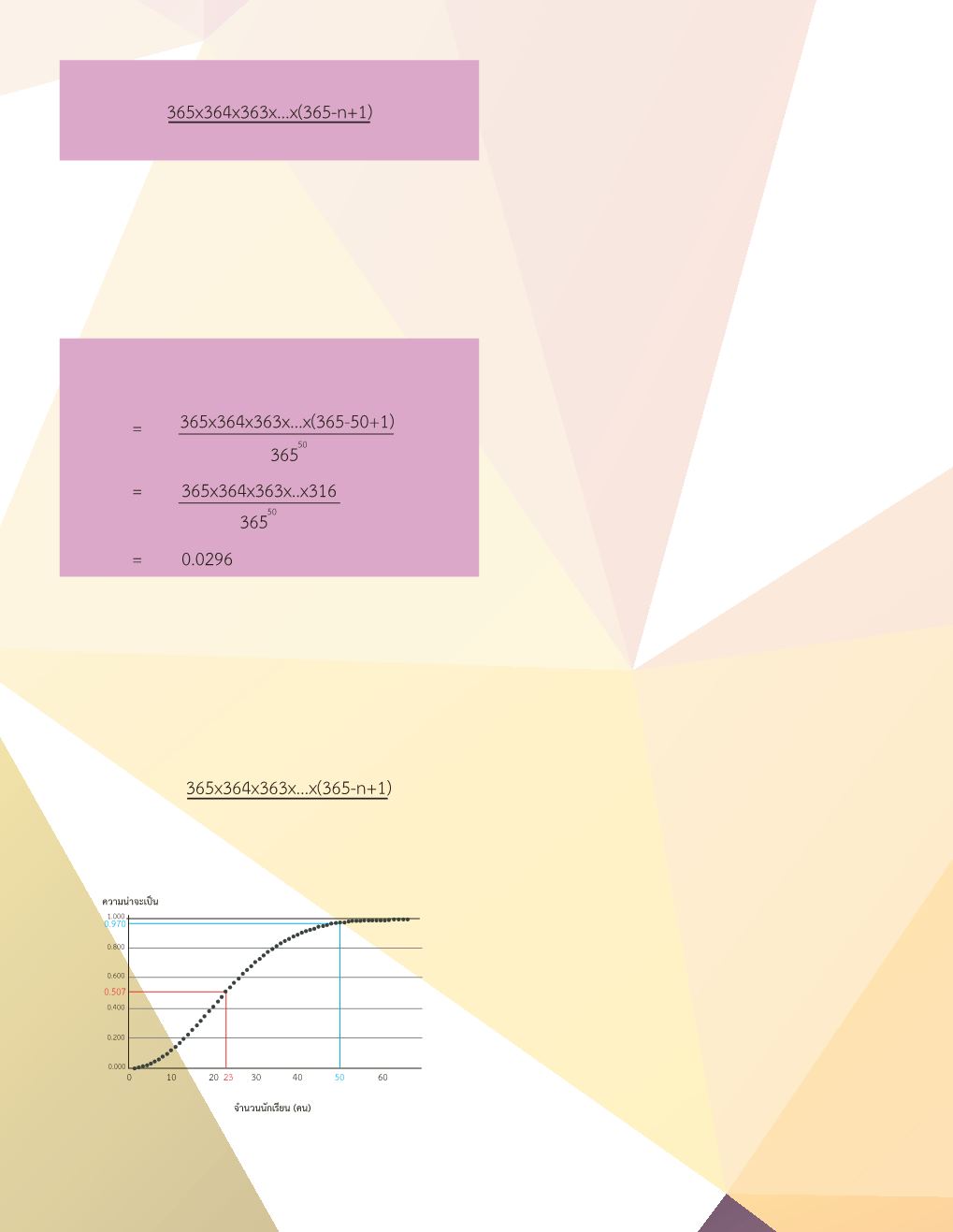
แล้วร่วมกันอภิปรายกับผู้เรียนว่าเหตุใดกราฟจึงมีลักษณะ
เช่นนี้ และตั้งค� ำถามเพิ่มเติมว่าจะต้องมีจ�ำนวนผู้เรียนเท่าใดจึง
จะท�ำให้ความน่าจะเป็นที่จะมีเพื่อนร่วมชะตามากกว่ากึ่งหนึ่ง
หรือ 0.5 ตามที่ได้ตั้งค�ำถามน�ำไว้ ซึ่งค�ำตอบคือต้องมีจ�ำนวน
ผู้เรียนตั้งแต่ 23 คนขึ้นไป
อย่างไรก็ดี หากการทดลองส� ำรวจหา ‘เพื่อนร่วมชะตา’ ของ
ผู้เรียนทั้งชั้นเรียนจ�ำนวน 50 คน พบว่าไม่มีใครที่เกิดวันและ
เดือนเดียวกันเลย ครูอาจอธิบายว่ากรณีนี้ยังสามารถเกิดขึ้นได้
เนื่องจากมีความน่าจะเป็นเท่ากับหนึ่งลบด้วยความน่าจะเป็นที่
จะมีเพื่อนร่วมชะตาอย่างน้อยหนึ่งคู่ หรือ 1 – 0.9704 ซึ่งมีค่า
เท่ากับ 0.0296 หรือประมาณ 2.96% ที่แม้จะมีค่าน้อยแต่ก็ยัง
มากกว่า 0 และมีโอกาสเป็นไปได้ และหากมีการสุ่มผู้เรียน
จ� ำนวน 50 คน หลาย ๆ ครั้งมากขึ้น โอกาสที่จะมี ‘เพื่อนร่วม
ชะตา’ ควรจะสูงกว่าโอกาสที่ไม่มี ‘เพื่อนร่วมชะตา’
กิจกรรมนี้ สามารถแสดงให้ เห็นได้ว่าการค� ำนวณทาง
คณิตศาสตร์มีส่วนช่วยให้เราประเมินสถานการณ์ต่าง ๆ ได้อย่าง
แม่นย� ำกว่าการคาดการณ์ด้วยสามัญส�ำนึก ซึ่งกิจกรรมนี้เป็น
กิจกรรมที่สามารถมองเห็นภาพได้ง่าย ใกล้ตัว และผู้เรียนทุกคน
สามารถมีส่วนร่วม โดยสามารถน�ำไปปรับใช้กับห้องเรียนที่มี
จ� ำนวนผู้ เรียนเท่ าใดก็ได้ โดยอาศัยสูตรทั่วไปในการหา
ความน่าจะเป็นเป็นเครื่องมือช่วยในการค�ำนวณ
ทั้งนี้เนื่องจากหากมีผู้เรียนเกิดในวันใดแล้ว คนถัด ๆ ไปจะ
ไม่สามารถมีวันเกิดในวันนั้นได้อีก ดังนั้นจ�ำนวนวิธีที่ผู้เรียน
จ�ำนวน n คนมีวันเกิดที่ไม่ซ�้ำกันเลยจะมี 365 x 364 x 363 x
… x (365 – n + 1) วิธี และเมื่อเทียบกับจ�ำนวนวิธีที่ผู้เรียน
จ�ำนวน n คนจะเกิดในวันต่าง ๆ ซึ่งมีทั้งหมด 365 วิธี แล้ว จะ
ได้ความน่าจะเป็นออกมาตามสูตรข้างต้น
ความน่าจะเป็นผู้เรียน n คนมีวันเกิดไม่ซ�้ ำกันเลย
ดังนั้นส�ำหรับนักเรียนจ�ำนวน 50 คน
ความน่าจะเป็นที่นักเรียน 50 คนมีวันเกิดไม่ซ�้ำกันเลย
ไปเขียนกราฟระหว่างจ�ำนวนนักเรียน n คน กับความน่าจะเป็น
ที่จะมีเพื่อนร่วมชะตา จะได้ดังรูปที่ 1
ปฏิทรรศน์มอนตีฮอลล์ เป็นปฏิทรรศน์คณิตศาสตร์ที่มีที่มา
จากเกมโชว์ทางโทรทัศน์ชื่อ Let’s Make a Deal ที่เคยออก
อากาศจริงในสหรัฐอเมริกา เมื่อช่วงปี ค.ศ. 1984-1986 โดย
ชื่อปฏิทรรศน์มอนตีฮอลล์ ก็คือ ชื่อของ พิธีกรรายการเกมโชว์นี้
นั่นเอง กติกาของเกมโชว์ Let’s Make a Deal หรือเกม
‘ประตูดวง’ มีอยู่ว่า มีประตูที่มีลักษณะเหมือนกันอยู่ 3 บานคือ
ประตู A B และ C โดยด้านหลังประตูทั้งสามนี้จะมีประตูเพียง
บานเดียวที่มีรถยนต์ ซึ่งเป็นของรางวัลใหญ่อยู่ และอีกสองบาน
ที่เหลือจะมีแพะเป็นรางวัลปลอบใจ ผู้เข้าแข่งขันสามารถเลือก
ประตูบานใดก็ได้ 1 บาน จากนั้นพิธีกรจะเลือกเปิดประตูที่มีแพะ
1 บาน แล้วถามผู้เข้าแข่งขันว่าจากประตูสองบานที่เหลือ เขาจะ
เปลี่ยนใจในการเลือกประตูหรือไม่ ถ้าคุณเป็นผู้เข้าแข่งขันควร
เลือกเปลี่ยนประตูหรือไม่เปลี่ยนประตู เพราะเหตุใด
นั่นคือ ความน่าจะเป็นที่ผู้เรียน 50 คนมีเพื่อนร่วมชะตา
อย่างน้อย 1 คู่ = 1 – 0.0296
= 0.9704
หรือ 97.04%
จากนั้นผู้สอนอาจน�ำสูตรการค�ำนวณหาความน่าจะเป็น
ที่นักเรียนจ�ำนวน n คนมีเพื่อนร่วมชะตา คือ
ความน่าจะเป็นที่นักเรียน n คนมีเพื่อนร่วมชะตา
รูปที่ 1 กราฟแสดงความสัมพันธ์ระหว่างจ�ำนวนนักเรียน n คน กับความน่าจะเป็นที่
จะมีเพื่อนร่วมชะตา (ที่มา:
The_Birthday_Problem)
365
= n
365
1- = n
n
20
นิตยสาร สสวท.
2 ปฏิทรรศน์มอนตีฮอลล์ (Monty Hall Paradox) กับกิจกรรม
เกม ‘ประตูดวง’