นิตยสาร สสวท. ฉบับที่ 193 มีนาคม - เมษายน 2558

21 / 62

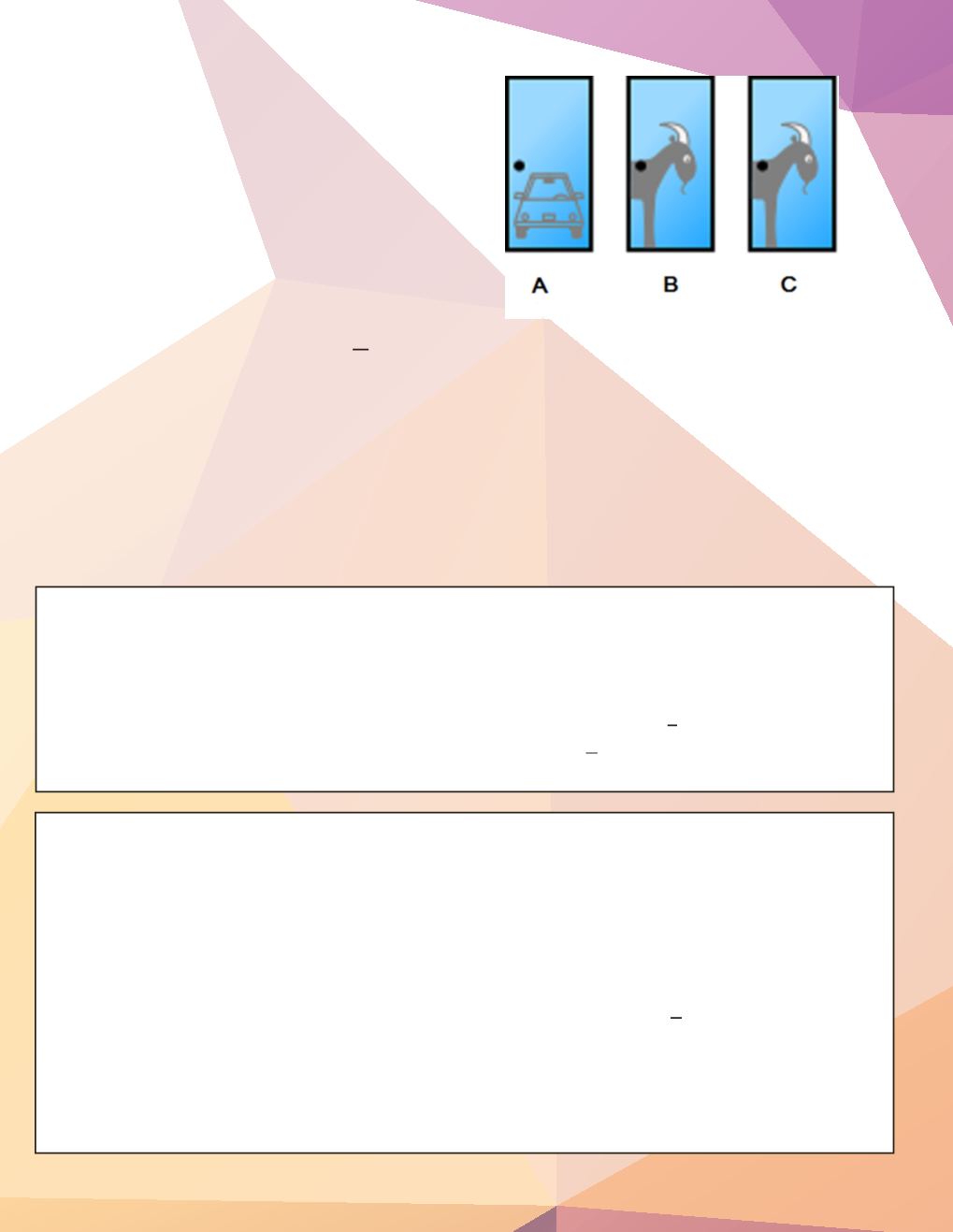
รูปที่ 2 แสดงตัวอย่างของเกมประตูดวง โดยสมมติให้รถยนต์
อยู่ที่ประตู A และให้ผู้แข่ งขันเลือกประตูนี้ จากนั้นคุณ
มอนตีฮอลล์จะเลือกเปิดประตูซึ่งไม่มีรถยนต์ ซึ่งจะเลือกได้
2 บานคือบาน B และบาน C โดยสมมติให้คุณมอนตีฮอลล์เลือก
เปิดประตู C ผู้เข้าแข่งขันจะได้รับโอกาสในการตัดสินใจอีกครั้ง
ว่าจะยังเลือกประตู A หรือจะเปลี่ยนเป็นประตู B ผู้เข้าแข่งขัน
ควรจะเปลี่ยนใจหรือไม่
จากปฏิทรรศน์มอนตีฮอลล์ในเกมประตูดวงนี้ หากใช้
สามัญส�ำนึกโดยทั่วไปในการพิจารณา คนส่วนใหญ่จะตอบว่า
ไม่จ�ำเป็นต้องเปลี่ยนใจเลือกประตูใหม่ เพราะโอกาสที่จะเลือก
ประตูได้ถูกต้องและได้รับรางวัลใหญ่ยังคงเป็น เช่นเดิม แต่
หากลองใช้หลักคณิตศาสตร์ด้านความน่าจะเป็นมาช่วยใน
การค�ำนวณแล้ว จะพบว่า การเลือดเปลี่ยนประตูจะท�ำให้โอกาส ที่จะชนะเพิ่มขึ้นเป็นสองเท่า ดังนั้นผู้แข่งขันควรเลือกเปลี่ยนประตู
ในทุกกรณีหลังจากที่พิธีกรได้เปิดประตูเฉลยออกมาแล้วหนึ่งบานและถามว่าจะเปลี่ยนใจหรือไม่เกมประตูดวงนี้นับเป็นเกมที่สร้าง
ความพิศวงทางคณิตศาสตร์ได้อย่างมาก เพราะแม้แต่บรรดานักคณิตศาสตร์ หรือครูอาจารย์ผู้ทรงคุณวุฒิทางคณิตศาสตร์เอง ก็ยัง
มีความรู้สึกที่ขัดแย้งกับความน่าจะเป็นที่ค�ำนวณได้จริง และมักตอบว่าไม่จ�ำเป็นต้องเปลี่ยนบานประตู ซึ่งปัญหานี้เคยเป็นที่ถกเถียง
และอธิบายกันอย่างกว้างขวางในวารสารทางคณิตศาสตร์ทั้งหลาย และเป็นตัวอย่างอันดีที่แสดงให้เห็นว่าบางครั้งสามัญส�ำนึก
ก็อาจลวงให้เราประเมินสถานการณ์ผิดพลาดไปได้อย่างง่าย ๆ เลยทีเดียว การค�ำนวณความน่าจะเป็นที่จะชนะของเกมประตูดวง
สามารถแสดงโดยแบ่งออกเป็นสองกรณีใหญ่ ๆ ดังนี้
ผู้เข้าแข่งขันเลือกประตูที่มีแพะตัวที่หนึ่ง -> พิธีกรเปิดประตูที่มีแพะตัวที่สอง -> ผู้เข้าแข่งขันเปลี่ยนใจไปเลือก
ประตูที่มีรถยนต์ท�ำให้ผู้เข้าแข่งขันเป็นฝ่ายชนะ
กรณี 1: อย่างไรก็ไม่เปลี่ยนใจ
ส�ำหรับกรณีที่ผู้เข้าแข่งขันไม่ยอมเปลี่ยนใจ โอกาสที่จะแพ้หรือชนะจะขึ้นอยู่กับการเลือกประตูในครั้งแรกเท่านั้น เพราะ
การเปิดประตูเฉลยและการเปิดโอกาสให้เปลี่ยนใจจากพิธีกรจะไม่มีผลใด ๆ ต่อไป เนื่องจากผลลัพธ์ของการเปิดประตูจาก
การเลือกประตูในครั้งแรกอาจเป็น แพะตัวที่หนึ่ง แพะตัวที่สอง หรือรถยนต์ ด้วยโอกาสที่เท่า ๆ กันดังนั้นความน่าจะเป็นที่
ผู้เข้าแข่งขันจะชนะ นั่นคือเลือกประตูที่มีรถยนต์ถูกต้องครั้งแรกแล้วไม่เปลี่ยนใจจึงเป็น และความน่าจะเป็นที่จะแพ้
นั่นคือเลือกประตูที่มีแพะตัวที่หนึ่งหรือตัวที่สองครั้งแรกแล้วไม่เปลี่ยนใจจึงเป็น
กรณี 2: อย่างไรก็จะเลือกประตูใหม่
ส�ำหรับกรณีที่ผู้เข้าแข่งขันเลือกที่จะเปลี่ยนใจ การเล่นเกมจะแบ่งออกเป็น 3 ขั้นตอนย่อย ๆ ดังนี้
1) ผู้เข้าแข่งขันเลือกประตูครั้งแรก
2) พิธีกรเลือกเปิดประตูที่มีแพะให้หนึ่งบานแล้วถามผู้เข้าแข่งขันว่าจะเปลี่ยนใจหรือไม่
3) ผู้เข้าแข่งขันเปลี่ยนใจไปเลือกประตูที่เหลือ โดยสามารถแยกคิดความน่าจะเป็นออกเป็นสามกรณีจากการเลือก
ครั้งแรกได้ดังนี้
กรณี 2.1: ผู้เข้าแข่งขันเลือกประตูที่มีแพะตัวที่หนึ่งเป็นครั้งแรก ซึ่งมีความน่าจะเป็นเท่ากับ เหตุการณ์จะมีกรณีเดียวดังนี้
รูปที่ 2 เกมประตูดวงจากปฏิทรรศน์มอนตีฮอลล์ (ที่มา:
wiki/Monty_Hall_problem)
1
3
1
3
1
3
2
3
ปีที่ 43 ฉบับที่ 193 มีนาคม - เมษายน 2558
21