นิตยสาร สสวท. ฉบับที่ 193 มีนาคม - เมษายน 2558

23 / 62

1
2
ซึ่งในการตัดสินใจว่าผู้เล่นควรจะเปลี่ยนใจหรือไม่นั้น จะต้อง
ใช้หลักการเรื่องความน่าจะเป็นและค่าคาดหมายมาพิจารณา
โดยอาจก� ำหนดให้ ในซองหนึ่งมีจ� ำนวนเงินอยู่ A บาท
ความน่าจะเป็นที่อีกซองหนึ่งจะมีจ�ำนวนเงินเป็น 2A และ จะ
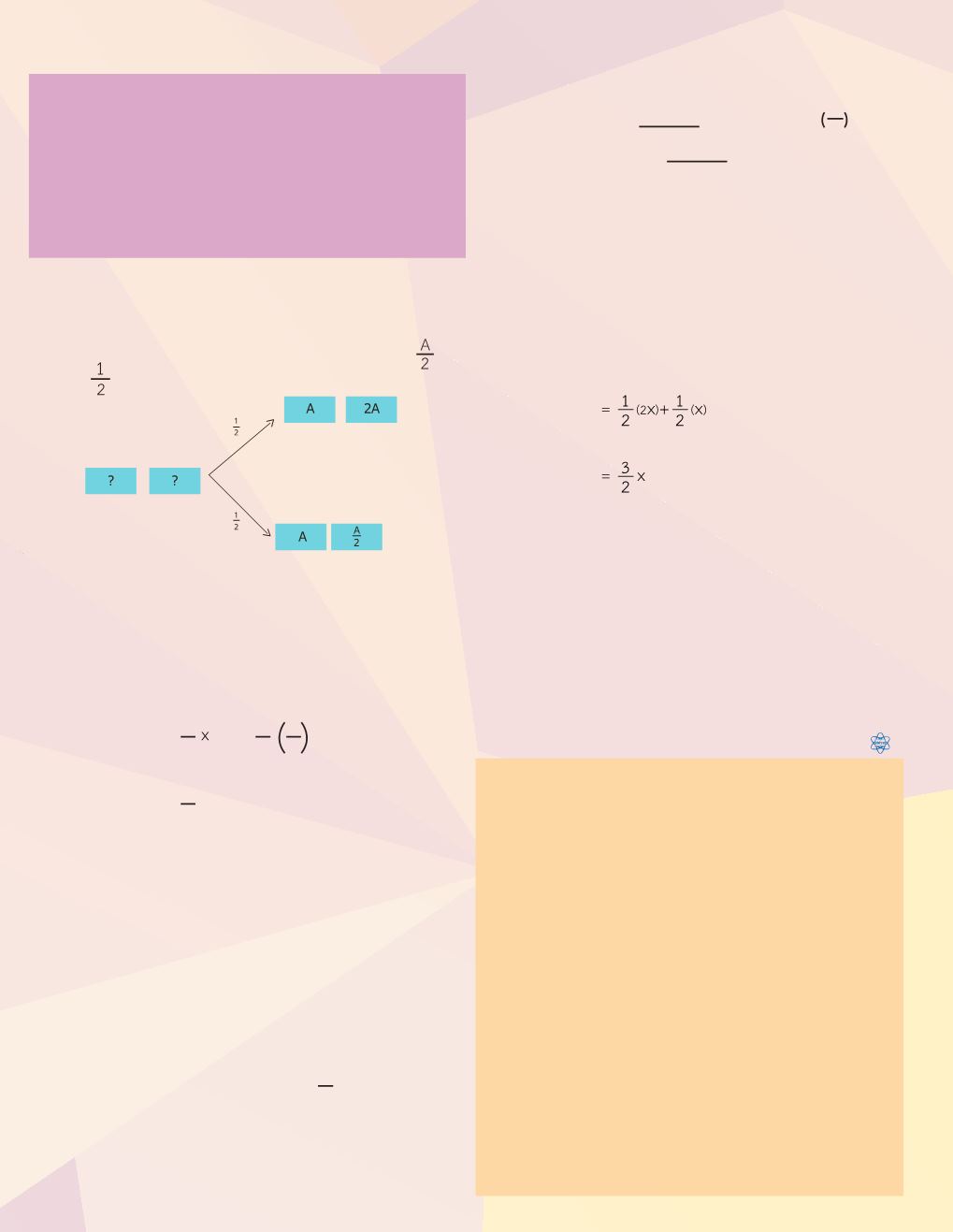
เท่ากับ เท่ากัน ดังแสดงในรูปที่ 3
รูปที่ 3 แผนภาพความน่าจะเป็นของกิจกรรม สุ่มซองสองเท่า
มีซองจดหมายที่มีลักษณะเหมือนกันทุกประการอยู่ 2 ซอง
และภายในซองทั้งสองนี้มีเงินบรรจุอยู่โดยในซองหนึ่งมีจ� ำนวน
เงินเป็นสองเท่าของอีกซองหนึ่งแต่ไม่ทราบว่าเป็นซองไหน ถ้า
ผู้เล่นสามารถเลือกหยิบซองจดหมายใดก็ได้เพื่อรับเงินในซองไป
แต่ได้รับโอกาสให้เปลี่ยนใจเลือกอีกซองหนึ่งก่อนจะเปิดซองอยู่
เสมอ ผู้เล่นควรตัดสินใจเปลี่ยนซองหรือไม่เพื่อให้มีโอกาสได้รับ
เงินที่มากกว่า เพราะเหตุใด
ปีที่ 43 ฉบับที่ 193 มีนาคม - เมษายน 2558
23
ถ้าในครั้งแรกผู้เล่นเลือกซองที่มีเงิน A บาท เรา
สามารถพิจารณาค่าคาดหมายของจ�ำนวนเงินที่อยู่ในอีกซอง
หนึ่งเพื่อเปรียบเทียบกันได้ดังนี้
ค่าคาคหมายของจ�ำนวนเงินที่อยู่ในอีกซอง
ค่าคาดหมายของจ�ำนวนเงินที่อยู่ในแต่ละซอง
บาท
บาท
บาท
บาท
ซึ่งมีค่ามากกว่า A บาท ดังนั้น จึงควรเลือกเปลี่ยนซอง
เพราะค่าคาดหมายของจ�ำนวนเงินสูงกว่า
ปัญหาจากการค�ำนวณค่าคาดหมายดังแสดงไว้ข้างต้น
อยู่ที่กลลวงของการน�ำเอาสองกรณีความน่าจะเป็นที่ต่าง
สถานการณ์กันมาร่ วมกันค�ำนวณเป็นค่ าคาดหมายเดียว
จากสมการจะสังเกตเห็นได้ว่าจากนิพจน์ (2A) ค่า A เป็น
ตัวแปรแทนจ�ำนวนเงินที่น้อยกว่า ในขณะที่นิพจน์ ค่า A
เป็นตัวแปรแทนจ�ำนวนเงินที่มากกว่า ดังนั้นตัวแปร A ที่ใช้ใน
สมการนี้ใช้แทนค่าสิ่งที่แตกต่างกัน จึงไม่สามารถน�ำมาค�ำนวณ
ร่วมกับความน่าจะเป็นเพื่อหาค่าคาดหมายได้
วิธีการค�ำนวณค่าคาดหมายที่ถูกต้องจะต้องก�ำหนด
ตัวแปรใหม่ให้ชัดเจน เช่น ก�ำหนดให้ X แทนจ�ำนวนเงินในซอง
ที่น้อยกว่า ดังนั้นจ�ำนวนเงินที่อยู่ในซองที่มากกว่าจะเป็น 2X
บาท เมื่อค�ำนวณค่าคาดหมายใหม่โดยจะต้องพิจารณาจากค่า
คาดหมายของจ�ำนวนเงินที่อยู่ในแต่ละซอง จะได้ว่า
แต่ก่อนจะเปิดซองที่เปลี่ยนใจมาแล้วหนึ่งครั้งผู้เล่นจะ
ได้รับโอกาสในการเปลี่ยนใจอีก ซึ่งหากพิจารณาค่าคาดหมาย
ในลักษณะเดียวกันจะพบว่าการเปลี่ยนใจเพื่อกลับไปเลือกซอง
เดิมอีกครั้งจะได้ค่าคาดหมายสูงกว่าเดิม จึงควรเลือกเปลี่ยนใจ
และจะเลือกเปลี่ยนใจสลับกันเช่นนี้เรื่อยไป โดยไม่สิ้นสุดจนไม่
สามารถสรุปได้ ว่ าควรจะ เ ลือกซอง ใดดีซึ่งขัดแย้ งกับ
สามัญส�ำนึกเบื้องต้นว่าเพียงเลือกซองใดซองหนึ่งโดยไม่เปลี่ยนใจ
โอกาสที่จะได้เงินจ�ำนวนมากกว่าก็เท่ากับ อยู่แล้ว
ซึ่งมีค่าน้อยกว่า 2X ซึ่งเป็นจ�ำนวนเงินจริงที่อยู่ใน
อีกซอง จึงไม่จ�ำเป็นต้องตัดสินใจเปลี่ยนซองจดหมาย
ปฏิทรรศน์ จดหมายสองซองนี้แสดง ให้ เห็นถึง
ความส�ำคัญในการแยกกรณีเหตุการณ์ความน่าจะเป็นและ
การก�ำหนดตัวแปรที่ชัดเจนในการหาค่าคาดหมาย โดยต้องไม่
รวมเอาสถานการณ์ที่เกิดจากการสมมติสองสิ่งที่แตกต่างกันมา
ค�ำนวณค่าคาดหมายร่วมกันซึ่งก็เป็นความผิดพลาดที่อาจท�ำให้
ค�ำตอบที่ได้ขัดแย้งกับสามัญส�ำนึกที่ถูกต้องอยู่แล้วไป กลายเป็น
ความไขว้ เขวที่ชวนให้ สงสัยว่ าบางครั้งสามัญส� ำนึกกับ
คณิตศาสตร์ที่ผิดพลาดก็อาจน�ำพาเราไปคนละทางได้จริง ๆ!
บรรณานุกรม
Micro-g environtment. (2014). สืบค้นเมื่อ 15 กันยายน 2557
จาก
#mediaviewer
Simon, Scott (2005). Math Guy: The Birthday Problem. สืบค้น
เมื่อ 7 ตุลาคม 2557,จา
story. php?storyId=4542341
Shermer, Michael (2009). The 3-Door Monty Hall Problem.
สืบค้นเมื่อ 7 ตุลาคม 2557, จาก
ty-hall-problem
Turner, Rich & Quilter, Tom. The Two Envelopes Problem.
สืบค้นเมื่อ 7 ตุลาคม 2557, จาก .
uk / - turner / notes / twoenvelopes / 2enulps.dpf
สถาบันส่งเสริมการสอนวิทยยาศาสตร์และเทคโนโลยี.(2554).
หนังสือเรียนรายวิชาพื้นฐานคณิตศาสตร์เล่ม ๒ ชั้นมัธยมศึกษา
ปีที่ ๓.กรุงเทพ: องค์การค้าของ สกสค.
สถาบันส่งเสริมการสอนวิทยยาศาสตร์และเทคโนโลยี.(๒๕๕๕).
คู่มือครู รายวิชาพื้นฐาน คณิตศาสตร์ เล่ม ๒ ชั้นมัธยมศึกษา
ปีที่ ๓. กรุงเทพ: องค์การค้าของ สกสค.
+
(2A)
A
1
2
= 54
1
2 2 =
A
2
A