
32
นิตยสาร สสวท.
แรงโน้มถ่วงระหว่างตัวเรากับโลกช่วยให้เราวัดมวลของโลก
ได้ เพราะว่าจาก (2)
g = GM
R
2
หรือ M = gR
2
………….. (3)
G
เราสามารถวัด g บนพื้นโลกได้ด้วยวิธีง่าย ๆ กล่าวคือ
จับเวลา t ในการปล่อยลูกปืนจากที่สูง h จนถึงพื้น จะได้
g = 2h
t
2
= 9.8 ms
-2
โลกของเรามีรัศมี R = 6,371 km = 6.371 × 10
6
m
แทนค่า g, R, G ใน (3) จะได้ M = 6 × 10
24
kg
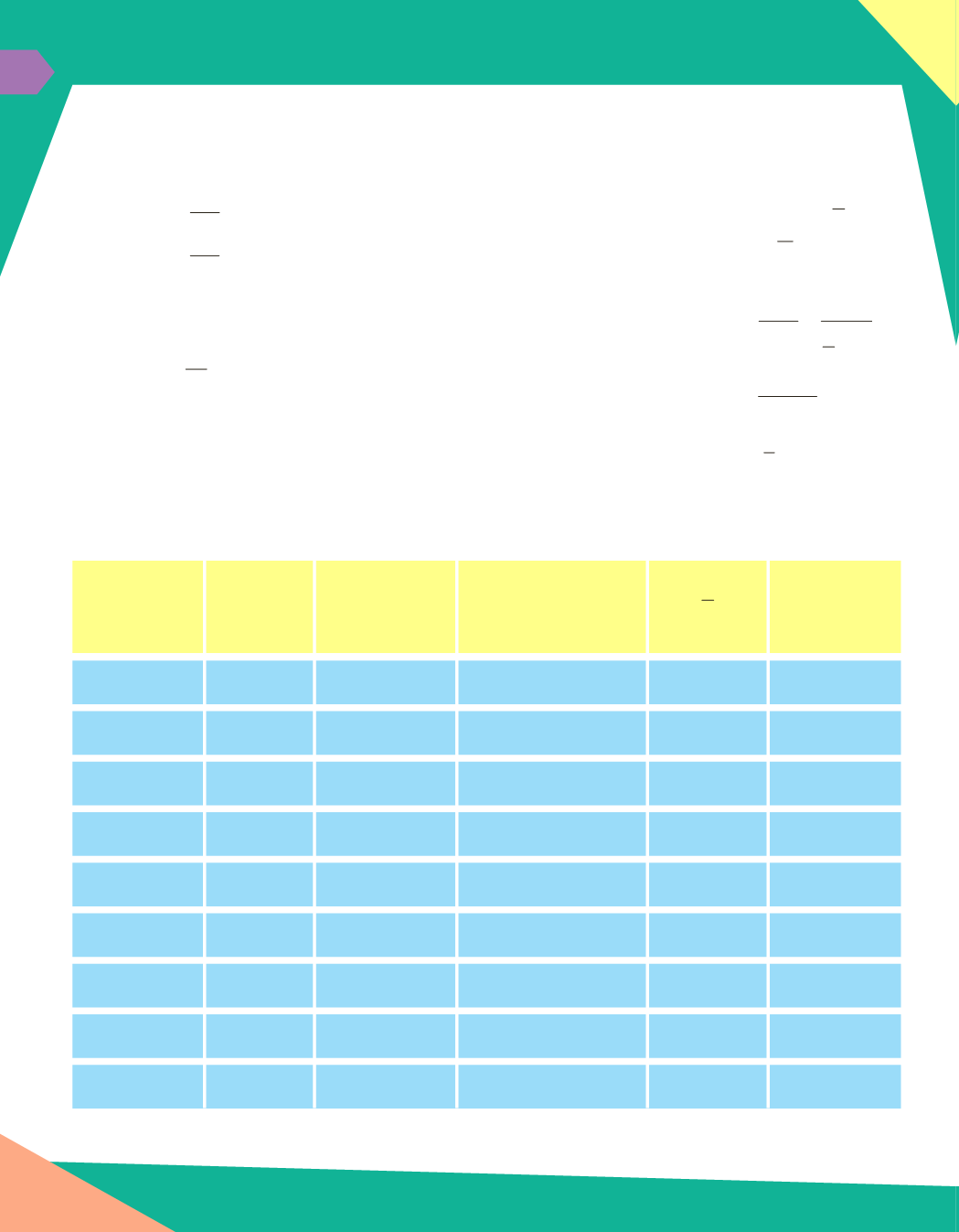
ตารางที่ 1
ความหนาแน่น รัศมี ความเร่งเนื่องจากแรงโน้มถ่วงที่ผิว และมวลของดาวเคราะห์
ดาวเคราะห์และ
ดวงจันทร์
รัศมี R
(10
3
m)
ความหนาแน่น
ρ
(10
3
kg m
-3
)
ความเร่งเนื่องจาก
แรงโน้มถ่วงที่ผิว g
(9.8 m s
-2
)
g
R
(10
-6
s
-2
)
มวล M
(6 × 10
24
kg)
พุธ
2,440
5.43
0.38
1.53
0.055274
ศุกร์
6,052
5.24
0.90
1.46
0.815005
โลก
6,371
5.52
1.00
1.54
1.000000
ดวงจันทร์
1,737
3.35
0.17
0.96
0.012300
อังคาร
3,396
3.94
0.38
1.10
0.107447
พฤหัสบดี 71,490
1.33
2.53
0.35
317.833
เสาร์
60,270
0.69
1.06
0.17
95.163
ยูเรนัส
25,560
1.27
0.90
0.35
14.536
เนปจูน
24,765
1.64
1.14
0.45
17.149
นั่นคือ มวลของโลกเท่ากับ 6 ล้านล้านล้านล้านกิโลกรัม
หรือ 6 พันล้านล้านล้านตัน
โลกเป็นทรงกลมรัศมี R มีปริมาตร (V) เท่ากับ
3
R
3
4
ดังนั้น ความหนาแน่นของโลก
ρ
= M
V
3
2
R
3
4
1
G
Rg
g
RG4
3
.......(4)
ρ
α
g
R
















