
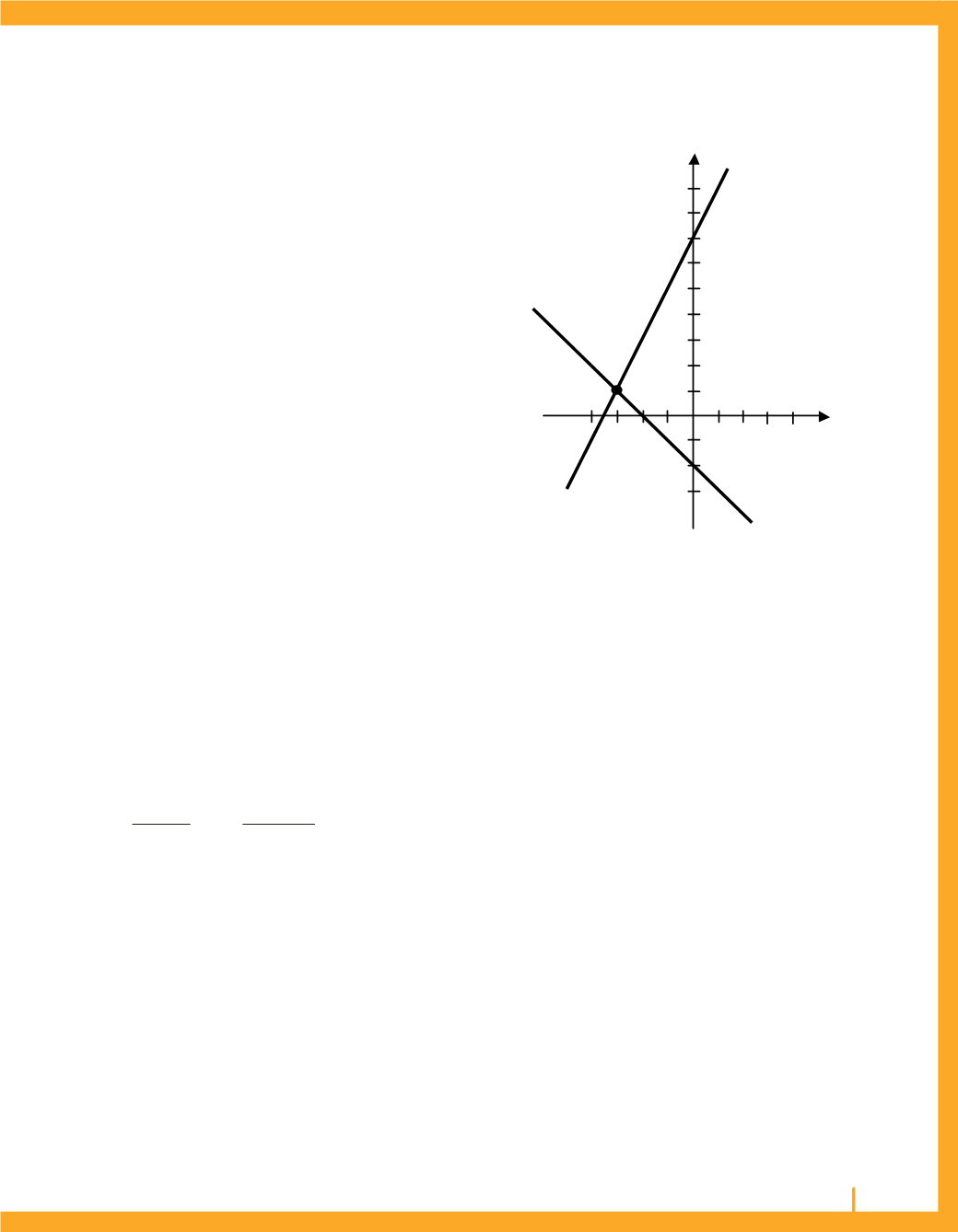
41
ปีที่ 41 ฉบับที่ 181 มีนาคม - เมษายน 2556
y = 2x+7
y
x
y =
–
x
–2
K
สำ
�หรับครูที่สอนเรื่องสมการเส้นตรง สามารถนำ
�ความรู้เรื่อง
นี้ทำ
�เป็นโครงงานนิทรรศการ เพื่อให้นักเรียนเล่นเป็นกิจกรรม
เสริมหลักสูตรได้ โดยแบ่งนักเรียนออกเป็นกลุ่ม ๆ ละ 6 คน ให้
ทั้ง 6 คน ที่อยู่ในกลุ่มเดียวกัน จับเป็นคู่ ๆ เพื่อแข่งขันกันคำ
�นวณ
หาความลับ K ผู้ที่ไขความลับได้ก่อนเป็นผู้ชนะ กิจกรรมนี้จะช่วย
ให้การเรียนสนุกสนานและจดจำ
�เนื้อหาได้แม่นยำ
�ขึ้น
ระบบแบ่งปันความลับแบบ 3–ใน–n
ทำ
�ได้โดยใช้หลักคณิตศาสตร์ง่าย ๆ เช่นกัน เป็นที่รู้กันว่า
จุด 3 จุด ใด ๆ บนระนาบ กำ
�หนดพาราโบลาได้เพียงพาราโบลา
เดียว สมการทั่วไปของพาราโบลาคือสมการกำ
�ลังสองที่อยู่ในรูป
y = a
0
+ a
1
x + a
2
x
2
……… (2)
จะเห็นว่าเมื่อ x = 0, y = a
0
แสดงว่า (0, a
0
) เป็นจุดที่
พาราโบลาตัดกับแกน y ดังนั้น เราเลือก a
0
บนแกน y ให้เป็น
ความลับ K และเลือกจุด n จุด บนพาราโบลานั้นที่ไม่ใช่จุด (0,
a
0
) มอบจุดเหล่านี้ให้ผู้เกี่ยวข้อง n คน เก็บไว้เป็นความลับส่วน
ของตน เมื่อสามคนใด ๆ นำ
�ความลับส่วนของตนมาประกอบ
กัน ก็จะสามารถหาสมการของพาราโบลานั้นได้ ซึ่งจะทำ
�ให้รู้ a
0
บนแกน y ที่เป็นความลับ K ได้ เพื่อความสะดวกในการอธิบาย
จะขอยกตัวอย่างการสร้างระบบแบ่งปันความลับแบบ 3-ใน-5
เมื่อได้สมการของเส้นตรง M แล้ว เจ้าหน้าที่สองคนนั้นจะ
ต้องหาจุดตัดของเส้นตรง L และ M ซึ่งจะต้องใช้ความรู้เรื่องการ
แก้สมการ หาผลเฉลยของระบบสมการเชิงเส้นที่มีสองตัวแปร
และมีสองสมการ ผลเฉลยที่ได้ก็คือจุดที่เป็นจุดตัดของเส้นตรง
L และ M นั่นเอง
ตัวอย่าง : ระบบแบ่งปันความลับแบบ 2–ใน–6
ในที่นี้ เราแบ่งข้อมูลที่เกี่ยวกับความลับ K ให้แก่คน 6 คน ซึ่ง
เมื่อนำ
�ส่วนความลับของ 2 คนใด ๆ ในจำ
�นวน 6 คนนี้มาประกอบ
กันแล้ว ทำ
�ให้สร้างหรือคำ
�นวณหาความลับ K ได้
1. สมมุติว่าเลือกจุด (–3, 1) ให้เป็นความลับ K
2. เลือก L ให้เป็นเส้นตรงซึ่งมีสมการ y = 2x + 7 โปรด
สังเกตว่าเส้นตรงนี้มีความชัน m = 2 และจุด (–3, 1) อยู่บนเส้น
ตรงนี้ สมการนี้ไม่เป็นความลับ สามารถประกาศให้สาธารณะรู้
ได้ แต่จุด (–3, 1) ต้องเก็บเป็นความลับ
3. เลือก y = –x – 2 ให้เป็นสมการของเส้นตรง M ซึ่งมี
ความชัน m = –1 และผ่านจุด (–3, 1) เก็บสมการของเส้นตรง
นี้ไว้เป็นความลับ
4. เลือกจุด (–4, 2), (–1, –1), (0, –2), (1, –3), (2, –4)
และ (3, –5) เป็นจุด 6 จุด บนเส้นตรง M มอบแต่ละจุดให้เจ้า
หน้าที่แต่ละคนซึ่งอยู่ในระบบ เจ้าหน้าที่แต่ละคนต้องเก็บจุดที่
ได้รับไว้เป็นความลับ
5. ในการหาเส้นตรง M สมมุติว่าเจ้าหน้าที่คนที่สองและ
คนที่ห้า ซึ่งได้รับจุด (–1, –1) และ (2, –4) ตามลำ
�ดับ เขาทั้ง
สองสามารถคำ
�นวณหาเส้นตรง M ได้โดยใช้สูตร (1) สำ
�หรับหา
สมการเส้นตรงที่ผ่านจุดสองจุด ดังนี้
y + 1 = –(x + 1)
y = –x – 2
6. ในการคำ
�นวณหาความลับ K เจ้าหน้าที่ทั้งสองจะต้องหาจุด
ตัดระหว่างเส้นตรง L และ M โดยแก้ระบบสมการต่อไปนี้
y = 2x + 7
สมการของเส้นตรง L
y = –x – 2
สมการของเส้นตรง M
นำ
�สมการสองไปลบออกจากสมการแรก จะได้
0 = 3x + 9
x = –3
แทนค่า x = –3 ใน y = –x – 2 จะได้ y = –(–3) – 2 = 1
ดังนั้น จุดตัดระหว่างเส้นตรง L และ M คือ K = (–3, 1) ดังรูป
=
y - (-1) –4 - (- 1)
x - (-1) 2 - (- 1)
















