นิตยสาร สสวท. ฉบับที่ 186 มกราคม - กุมภาพันธ์ 2557

12 / 62

m
m
0 x =
m m
m
mg x k
=
2 mg x k
=
h
(a) (b) (c) (d) (e)
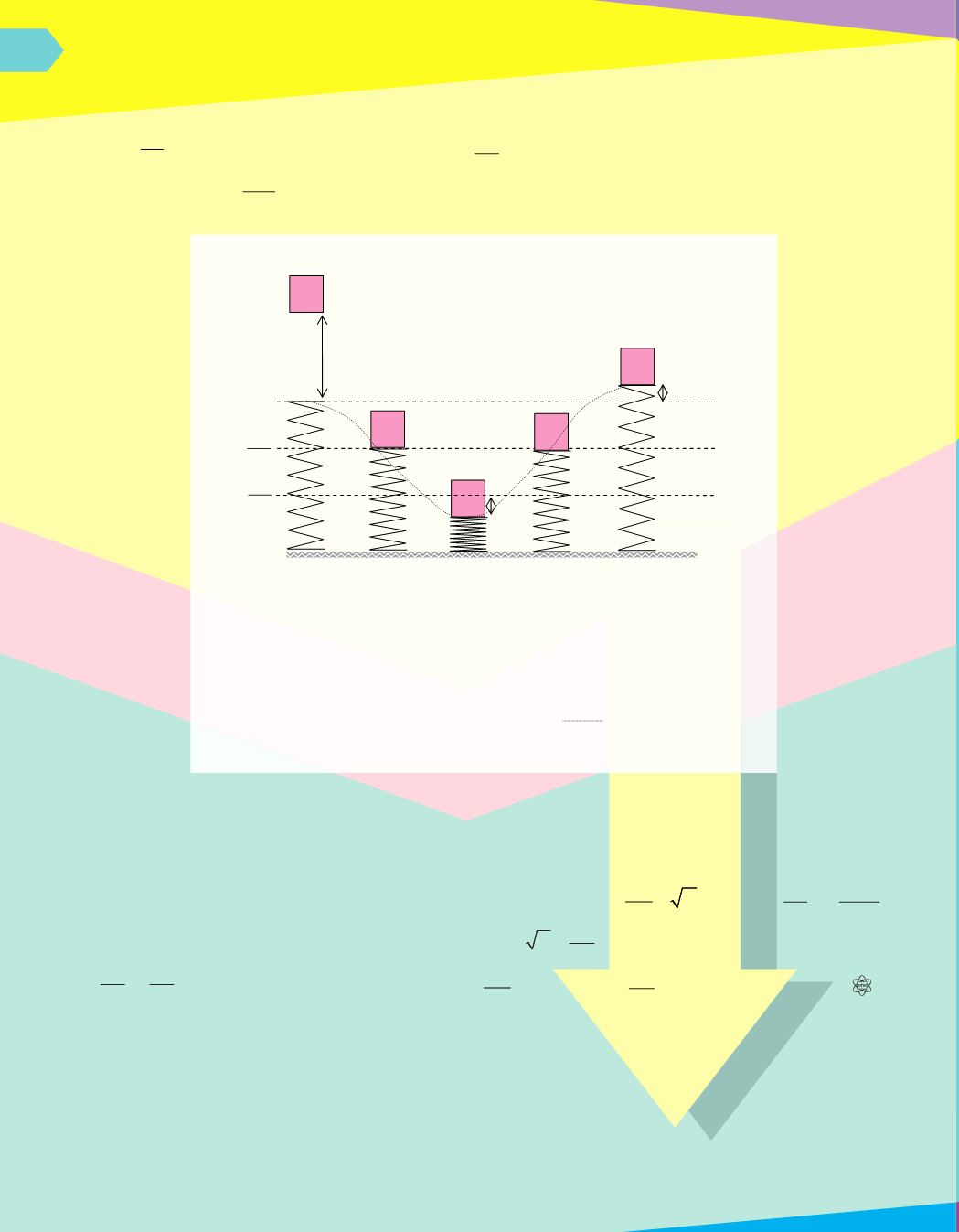
จากรูป (a) ปลอยวัตถุที่ตำแหน งสูง h จากปลายสปริง
(b) วัตถุกำลังเคลื่อนที่ผานตำแหน งสมดุลแรง x=mg/k แตไมหยุดนิ่งที่ตำแหนงนี้
เพราะยังมีสภาพเฉื่อยกอนเขาสูสมดุลแรง
(c) วัตถุหยุดนิ่งที่ตำแหนงต่ำสุด ซึ่งไมใช x=mg/k แตเปนที่ตำแหนง x=2mg/k+
(d) วัตถุเคลื่อนที่ขึ้นผานตำแหนงสมดุล
(e) ในกรณีที่มวลติดกับปลายสปริง มวลจะเคลื่อนที่ขึ้นไปหยุดที่ระยะยืดของสปริงเทากับ
ในกรณีที่มวลไมติดกับปลายสปริง มวลกอนดังกลาวก็จะขึ้นมาหยุดที่ตำแหนงปลอยในรูป (a) นั่นเอง
พื้น
สมมติวามวล m
ติดกับปลายสปริง
หลังสัมผัสกับสปริง
แรง ( mg x
k = ) เช่นเดิม แต่แอมพลิจูดการสั่นจะเปลี่ยนเป็น mg
k   นั่นคือสั่นแรงขึ้นด้วยระยะ  ดังนั้นต�าแหน่งต�่าสุดที่
ก้อนมวลลงไปได้คือ 2mg x
k    (แต่ถ้าก้อนมวลไม่ติดกับปลายสปริง ก้อนมวลก็จะเคลื่อนที่กลับมาที่ต�าแหน่งที่ปล่อย)
สรุป
สปริงตั้งอยู่ในแนวดิ่ง มีค่านิจสปริงเป็น k N/m ปล่อยก้อนมวล m จากระยะสูง h วัดจากปลายด้านบนของสปริง ก้อนมวล
m ตกลงที่ปลายสปริงและอัดสปริงลงไป สปริงจะหดสั้นมากที่สุดเป็นระยะเท่ากับ mg x R
k = ± โดยที่
2 2 mg mgh
R
k k
 
   
 
ถ้ามวลติดไปกับปลายสปริงหลังสัมผัส และเราอาจเขียน mg R
k    เราจะได้ว่าก้อนมวลสั่นอยู่ในช่วง
mg mg
x
k k
 
     
  นั่นคือเป็นการสั่นรอบ ๆ ต� าแหน่ง mg x
k = ด้วยแอมพลิจูด mg
k  
นิตยสาร สสวท.
12