
3.น�
ำครึ่งวงกลมวัดมุมวางบนกระดาษการ์ ดโดยให้
จุดกลางของครึ่งวงกลมอยู่ตรงมุมกระดาษการ์ดพอดี ให้ผู้สังเกตมอง
จุด X โดยดวงตาอยู่ระดับเดียวกับหน้าโต๊ะ โดยเริ่มมอง
จากทีละฝั่ง (อาจเริ่มจากฝั่งกระดาษการ์ด 1) ใช้ไม้บรรทัดเล็ง
ระยะไปที่จุด X แล้วให้เพื่อนช่วยอ่านค่ามุมที่เกิดจากเส้นฐาน
กับมุมที่ไม้บรรทัดเล็งไปที่จุด X ที่วัดได้จากครึ่งวงกลม บันทึก
ค่าไว้
4.ท�
ำเช่นเดียวกับข้อ 3. แต่เปลี่ยนเป็นมองจุด X จาก
ต�
ำแหน่งกระดาษการ์ด 2 ท�
ำการวัดมุม แล้วบันทึกค่าไว้
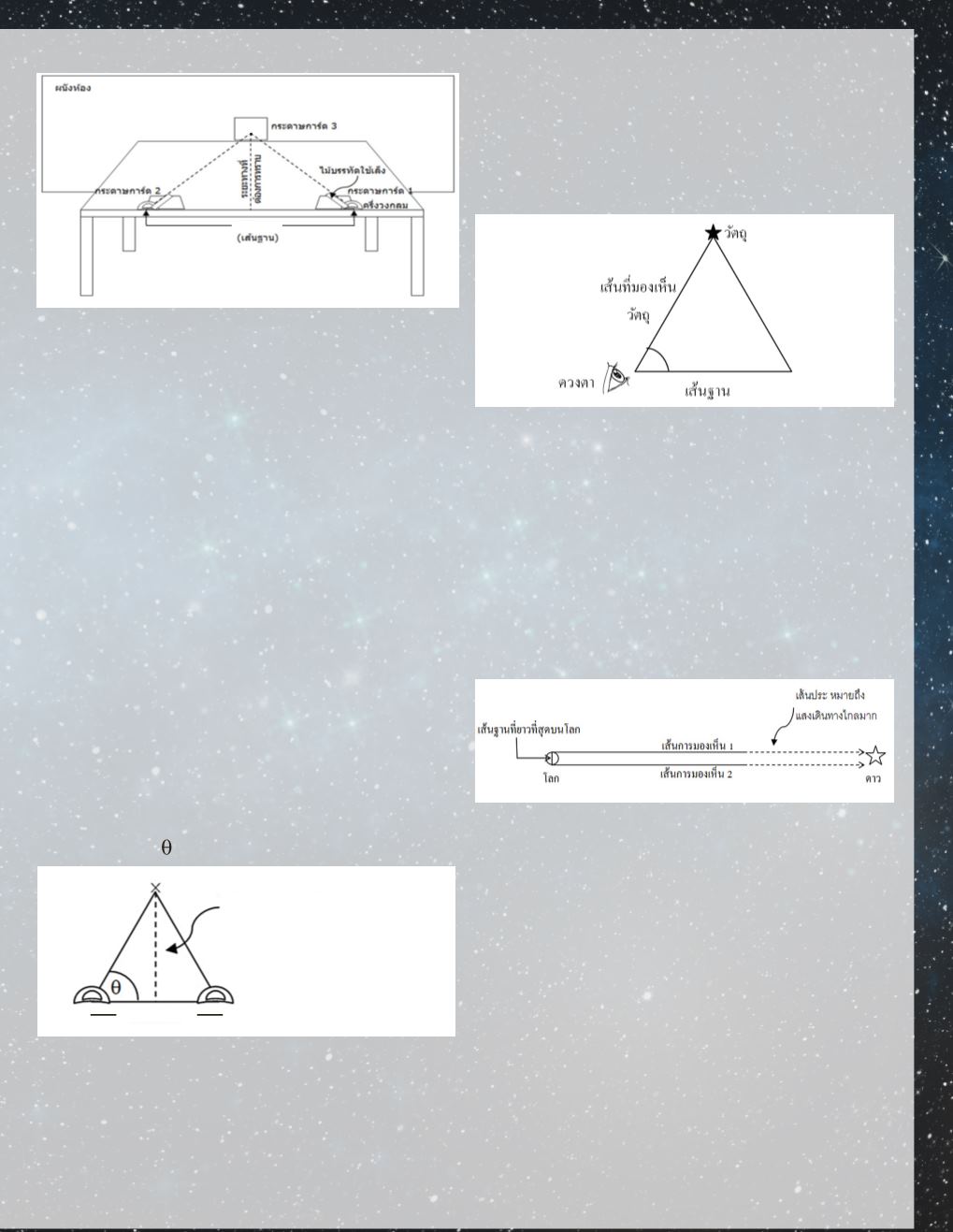
5.ค�
ำนวณหาระยะทางระหว่างจุดกึ่งกลางของเส้นฐานกับ
จุด X โดยวาดสามเหลี่ยมที่ได้จากการวัดเป็นสามเหลี่ยมย่อส่วน
ลงในกระดาษทด (อาจก�
ำหนดให้ 10 เซนติเมตร ในกระดาษทด
ของเราเท่ากับ 100 เซนติเมตร ในของจริง) น�
ำครึ่งวงกลมมาวาด
มุมให้เท่ากับที่วัดได้ลงที่ปลายเส้นฐานในกระดาษทด แล้วลาก
เส้นต่อทั้งสองด้านให้บรรจบกันจนเกิดเป็นสามเหลี่ยม ที่จุด
ปลายของสามเหลี่ยมคือต�
ำแหน่งของ X แล้ววัดระยะทางตั้งแต่
จุด X นี้จนถึงจุดกึ่งกลางของเส้นฐาน บันทึกค่าไว้ และค�
ำนวณ
กลับไปเป็นระยะทางจริงของจุด X กับจุดกึ่งกลางที่ท�
ำ
การทดลองบนโต๊ะ โดยการน�
ำ 10 ไปคูณกับระยะทางที่วัดได้ใน
สามเหลี่ยมภาพ 3 หรือค�
ำนวณส่วนสูงของสามเหลี่ยมจาก
ความสูง = 5 tan เซนติเมตร
เราสามารถใช้หลักการของสามเหลี่ยมข้างต้น มาใช้ในการหา
ระยะทางจากโลกถึงดวงดาวได้ นั่นคือ ลากเส้นฐานและวัดมุม
ที่เกิดจากเส้นฐานกับเส้นที่มองเห็นวัตถุ ดังภาพ 4
6.ทดลองวัดระยะทางจริงจากจุด X บนผนังห้องมาถึง
จุดกึ่งกลางของเส้นฐานที่วาดไว้บนโต๊ะ เทียบกับระยะทางที่ได้
จากการค�
ำนวณว่าใกล้เคียงกันหรือไม่ (ควรได้ค่าใกล้เคียงกัน)
ส�
ำหรับเส้นฐานที่ยาวที่สุดที่อยู่บนโลกมีค่า 12,742 กิโลเมตร
(เส้นผ่านศูนย์กลางของโลกนั่นเอง) แต่เนื่องจากระยะทาง
ดังกล่าวมีค่าน้อยมากแม้ว่าเทียบกับระยะทางจากโลกถึงดาวที่
ใกล้โลกที่สุด ซึ่งหมายความว่าเส้นฐานใด ๆ ก็ตามบนโลกนั้น
สั้นมาก!!! ด้วยเหตุนี้ เส้นการมองเห็นดวงดาวเมื่อผู้สังเกตอยู่ที่
ต�
ำแหน่งต่าง ๆ กันบนโลกจึงเป็นเส้นที่ขนานกัน ดังภาพ 5
ไม่ว่าจะสร้างเส้นฐานใด ๆ บนโลก เส้นการมองเห็นดวงดาว
จากแต่ละด้านของสามเหลี่ยมก็เป็นเส้นที่ยาวและแคบมากเสมอ
และมุมที่ฐานของสามเหลี่ยมแต่ละด้านดูเหมือนจะเป็นมุมเกือบ
90 องศา ดังนั้นในการหาระยะทางจากโลกถึงดวงดาว
นักดาราศาสตร์จึงใช้การถ่ายภาพและสร้างเส้นฐานที่ยาวกว่า
เส้นฐานบนโลกมาก ๆ ขึ้นมา
นักดาราศาสตร์ท�
ำการบันทึกเส้นการมองเห็นดวงดาวที่อยู่
ใกล้โลกจากต�
ำแหน่งหนึ่งบนโลก จากนั้น เมื่อเวลาผ่านไป 6
เดือน จึงท�
ำการสังเกตดาวดวงเดิมอีกครั้งจากต�
ำแหน่งเดิม
บนโลก ท�
ำไมต้อง 6 เดือน? นั่นเป็นเพราะโลกของเราจะโคจร
ไปอยู่อีกฝั่งหนึ่งของดวงอาทิตย์พอดีนั่นเอง
ภาพ 2 วิธีวัดระยะทางแบบโดยอ้อม
ภาพ 3 วิธีหาระยะทางในกระดาษทด
ภาพ 4 หลักการสามเหลี่ยมที่ประยุกต์ใช้ในการหาระยะทางจากโลกถึง
ดวงดาว
ภาพ 5 ภาพวาดแสดงเส้นการมองเห็นสองเส้นจากโลกจะขนานกัน
หมายเหตุ: ยกเว้นดาวที่อยู่ใกล้ ได้แก่ ดวงอาทิตย์ และดวงจันทร์ เป็นต้น
4. วิธีวัดระยะทางจากโลกถึงดวงดาว
10 เซนติเมตร
ใช้ไม้บรรทัดวัดระยะทางโดยตรง
100 เซนติเมตร
x
13
ปีที่ 43 ฉบับที่ 194 พฤษภาคม - มิถุนายน 2558
















