
40
นิตยสาร สสวท
• ส่วนของเส้นตรง A
0
A แทนข้อเหวี่ยง ซึ่งเป็น
ชิ้นส่วนที่ท�ำหน้าที่ส่งก�ำลังไปยังชิ้นส่วนอื่นๆ
เพื่อท�ำให้กลไกเคลื่อนไหวหรือก้าวเดิน
• จุด A
0
และ B
0
เป็นจุดตรึงที่อยู่บนตัวหุ่นยนต์
• รูปสามเหลี่ยม BB
0
C แทนขาท่อนบน
• รูปสามเหลี่ยม DEF แทนขาท่อนล่างโดยจุด F
เป็นเท้า
• รูปสี่เหลี่ยม B
0
CDE ท�ำหน้าที่คล้ายข้อเข่าใน
การก้าวเดิน
• ส่วนของเส้นตรง AB และ AE ท�ำหน้าที่เป็น
กล้ามเนื้อและเส้นเอ็นในการควบคุมการก้าวเท้า
การออกแบบกลไกการก้าวเดินของเท้าได้รับ
การอ้างอิงจากแบบโครงร่างของกลไกเตโอยันเซินที่แสดงใน
รูปที่ 2 ข)
การออกแบบกลไกนี้มีจุดประสงค์ที่จะท�ำให้
เส้นทางการเคลื่อนของเท้า (จุด F) มีลักษณะคล้ายวงรี
ด้วยเหตุผลสองประการคือ 1) วงรีเป็นเส้นทางที่สามารถ
ท�ำให้หุ่นยนต์ก้าวข้ามสิ่งกีดขวางขนาดเล็กได้โดยที่ตัวหุ่นยนต์
ไม่เสียการทรงตัว และ 2) ลดเสียงดังที่เกิดจากการกระทบกัน
ระหว่างชิ้นส่วน อันเนื่องมาจากแรงเฉื่อยขณะเดิน
เส้นทางการเคลื่อนที่ของเท้าแต่ละก้าวสามารถ
แบ่งออกได้เป็นสองส่วน ดังแสดงในรูปที่ 3 ส่วนที่หนึ่งเป็น
ส่วนของการออกแรงผลักดันให้เคลื่อนที่ (ระหว่างจุด P ถึง
จุด Q) ซึ่งในส่วนนี้เท้าจะสัมผัสกับพื้น ส่วนที่สองเป็นส่วน
ของการก้าวเท้า ซึ่งเท้าจะไม่สัมผัสกับพื้น ระยะจากจุด P
ถึงจุด Q จะเป็นความยาวหนึ่งก้าวเดิน และความสูงของ
การยกเท้าก็คือความสูงมากที่สุดของสิ่งกีดขวางที่หุ่นยนต์
จะก้าวข้ามไปได้
รูปที่ 3
เส้นทางการเคลื่อนที่ของเท้า (จุด F)
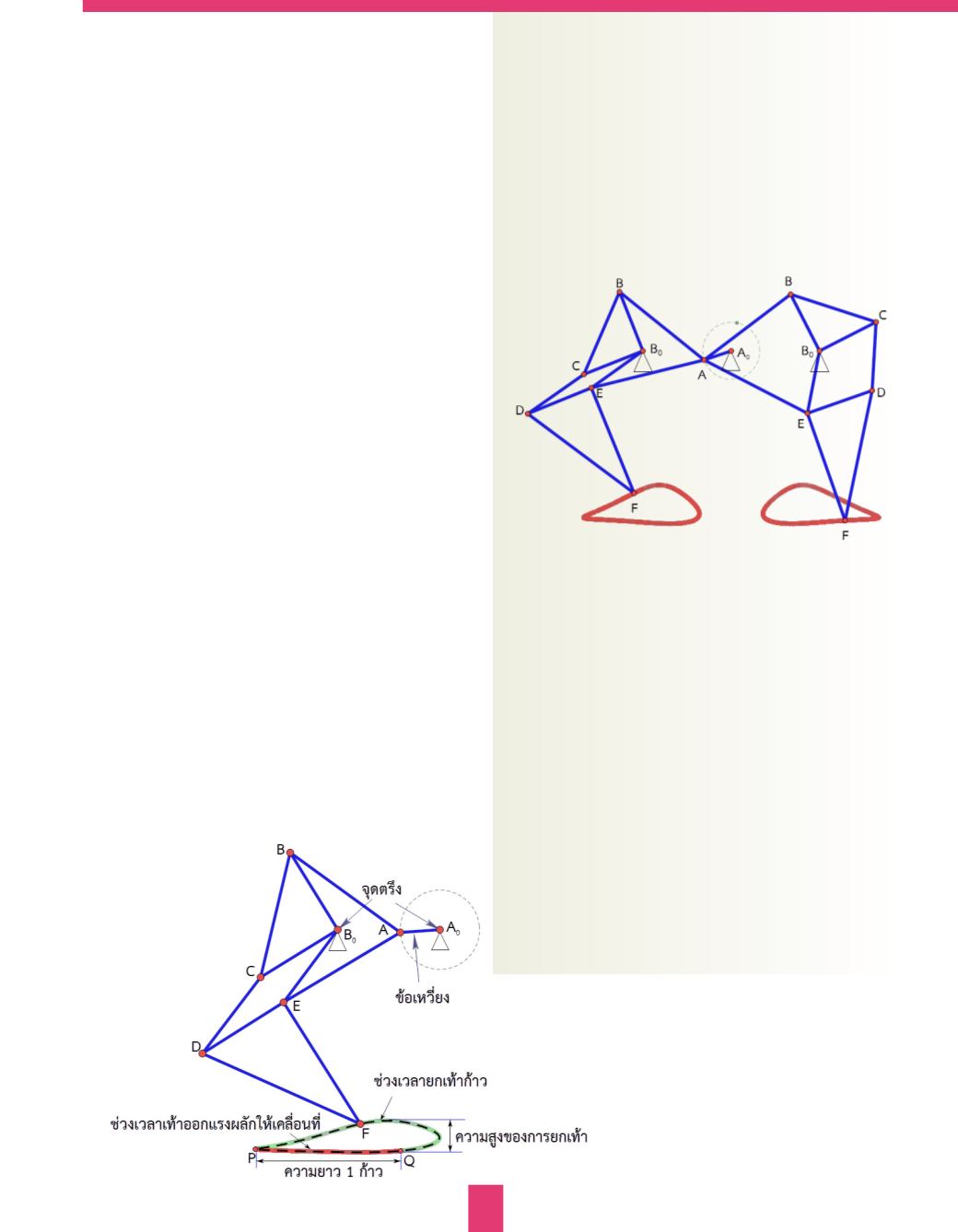
รูปที่ 4
กลไกเตโอยันเซินเมื่อประกอบเป็นขาสองข้าง
กลไกเตโอยันเซินเป็นกลไกที่ได้รับการออกแบบ
เพื่อเปลี่ยนการเคลื่อนที่แบบหมุนเป็นการเคลื่อนไหว
ของขา เมื่อน�ำกลไกเตโอยันเซิน 2 ชุดที่เหมือนกัน
มาประกอบเรียงกันดังรูปที่ 4 แล้วให้จุด A หมุนรอบจุด A
0
จะท�ำให้กลไกท�ำงานเหมือนกับการก้าวเดินของขาสองข้าง
พื้นฐานการท�ำงานของขาทั้งสองอยู่ที่ระยะสัมพัทธ์ของ
จุดต่อทั้ง 12 จุด (จุดตรึง 3 จุด ให้เท่ากับ 1 จุด)
รายละเอียดของกลไก
การจ�ำลองกลไกเตโอยันเซินด้วยโปรแกรม
Geometer's Sketchpad (GSP)
การสร้างกลไกการก้าวเดินของขาของหุ่นยนต์
สิ่งส�ำคัญคือขนาดของชิ้นส่วนแต่ละชิ้นที่เมื่อประกอบ
กันแล้ว และมีการเคลื่อนไหวจะท�ำให้ได้เส้นทางการ
เคลื่อนไหวของจุดที่แทนเท้าเป็นไปตามรูปแบบที่ต้องการ
โปรแกรม GSP เป็นโปรแกรมที่สร้างขึ้นมา
เพื่อใช้เป็นเครื่องมือในการเรียนการสอนคณิตศาสตร์
แบบพลวัต ท�ำให้เข้าใจแนวความคิดทางคณิตศาสตร์
ที่ถูกต้อง จึงเห็นความเกี่ยวเนื่องระหว่างเรขาคณิตกับ
พีชคณิตได้อย่างเป็นรูปธรรม ด้วยสมบัติที่เป็นพลวัต


















