
23
ปีที่ 46 ฉบับที่ 211 มีนาคม - เมษายน 2561
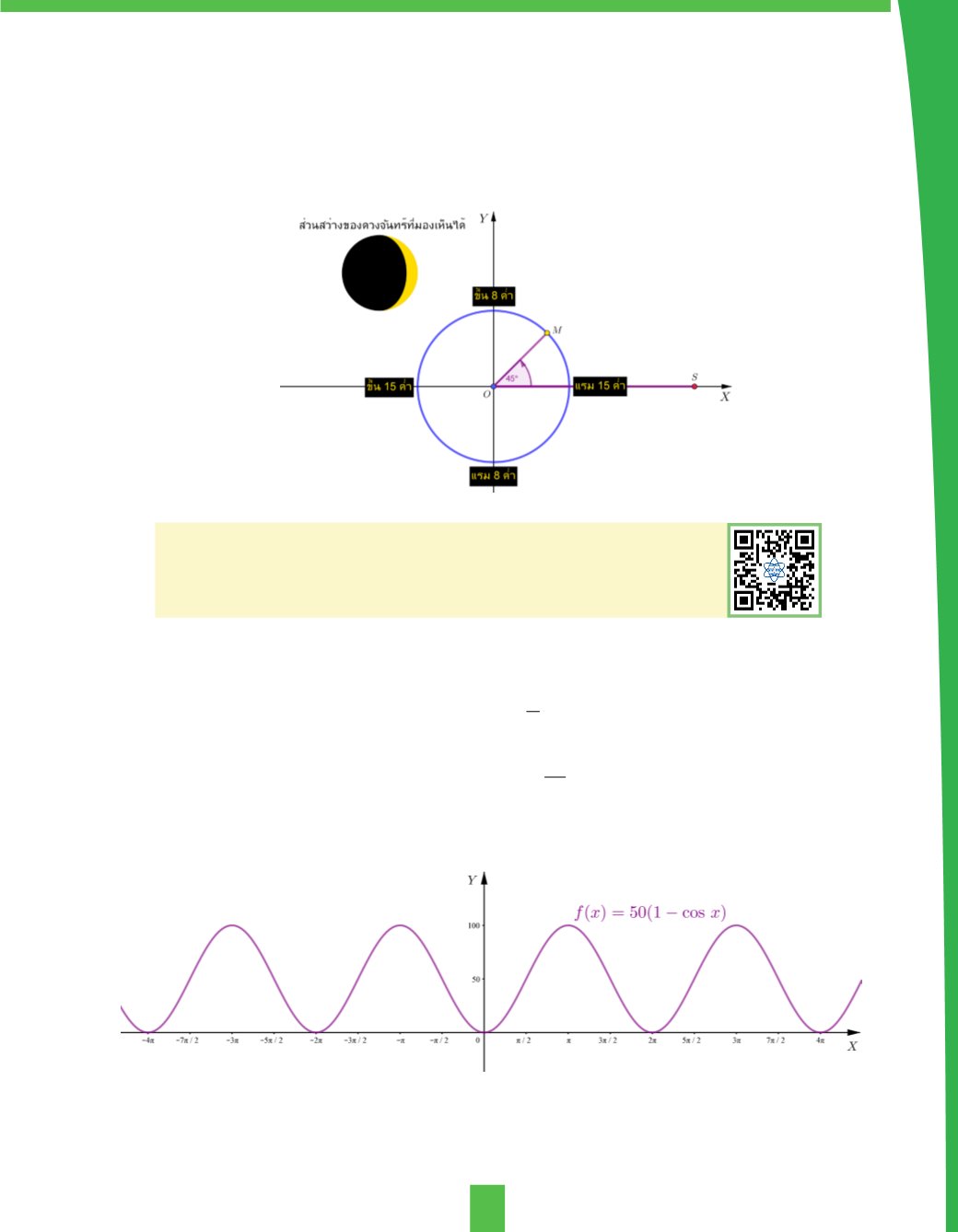
ดังนั้นจะเห็นได้ว่าปรากฏการณ์ข้างขึ้นข้างแรมมีลักษณะเทียบเคียงได้กับพฤติกรรมของฟังก์ชันตรีโกณมิติ ซึ่งเป็น
ฟังก์ชันที่เป็นคาบดังที่กล่าวในตอนต้น ถ้าสมมติให้วงโคจรของดวงจันทร์รอบโลกเป็นวงกลม และก�ำหนดให้โลกอยู่ที่
จุดก�ำเนิด
�
ดวงจันทร์อยู่ที่จุด
�
ดวงอาทิตย์อยู่ที่จุด และ
�
แทนมุม
�
�
จะสามารถจ�ำลองการเกิดปรากฏการณ์
ข้างขึ้นข้างแรมได้ดังรูป
หมายเหตุ
สามารถเข้าไปที่เว็บไซต์
https://www.geogebra.org/m/TbT5zz75เพื่อดูภาพเคลื่อนไหวของกราฟจ�ำลองปรากฏการณ์ข้างขึ้นข้างแรม
โดยเมื่อเทียบกับ
ภาพ 2
จะได้ว่า
เมื่อ
0
x
=
จะเป็นวันที่ดวงจันทร์อยู่ระหว่างโลกกับดวงอาทิตย์ หรือวันแรม 15 ค�่ำ
เมื่อ
0
x
π
< <
จะเป็นข้างขึ้น โดยเมื่อ
2
x
π
=
จะเป็นวันขึ้น 8 ค�่ำ
เมื่อ
x
π
=
จะเป็นวันขึ้น 15 ค�่ำ
เมื่อ
2
x
π
π
< <
จะเป็นข้างแรม โดยเมื่อ จะเป็นวันแรม 8 ค�่ำ
ถ้าให้
( )
(
)
50 1 cos
f x
x
= −
เป็นฟังก์ชันแสดงร้อยละของส่วนสว่างของดวงจันทร์ที่สามารถ
มองเห็นได้ จะสามารถเขียนกราฟของ
f
ได้ดังนี้
3
2
x
π
=
ภาพ 3
กราฟจ�ำลองการเกิดปรากฏการณ์ข้างขึ้นข้างแรม
ภาพ 4
กราฟของฟังก์ชัน
f
จะเห็นว่า โดเมนของฟังก์ชัน
f
คือ เซตของจ�ำนวนจริง เรนจ์ของฟังก์ชัน
f
คือ [0,100] คาบของฟังก์ชัน
f
คือ
2
π
และแอมพลิจูดของฟังก์ชัน
f
คือ 50


















