
25
ปีที่ 42 ฉบับที่ 189 กรกฎาคม- สิงหาคม 2557
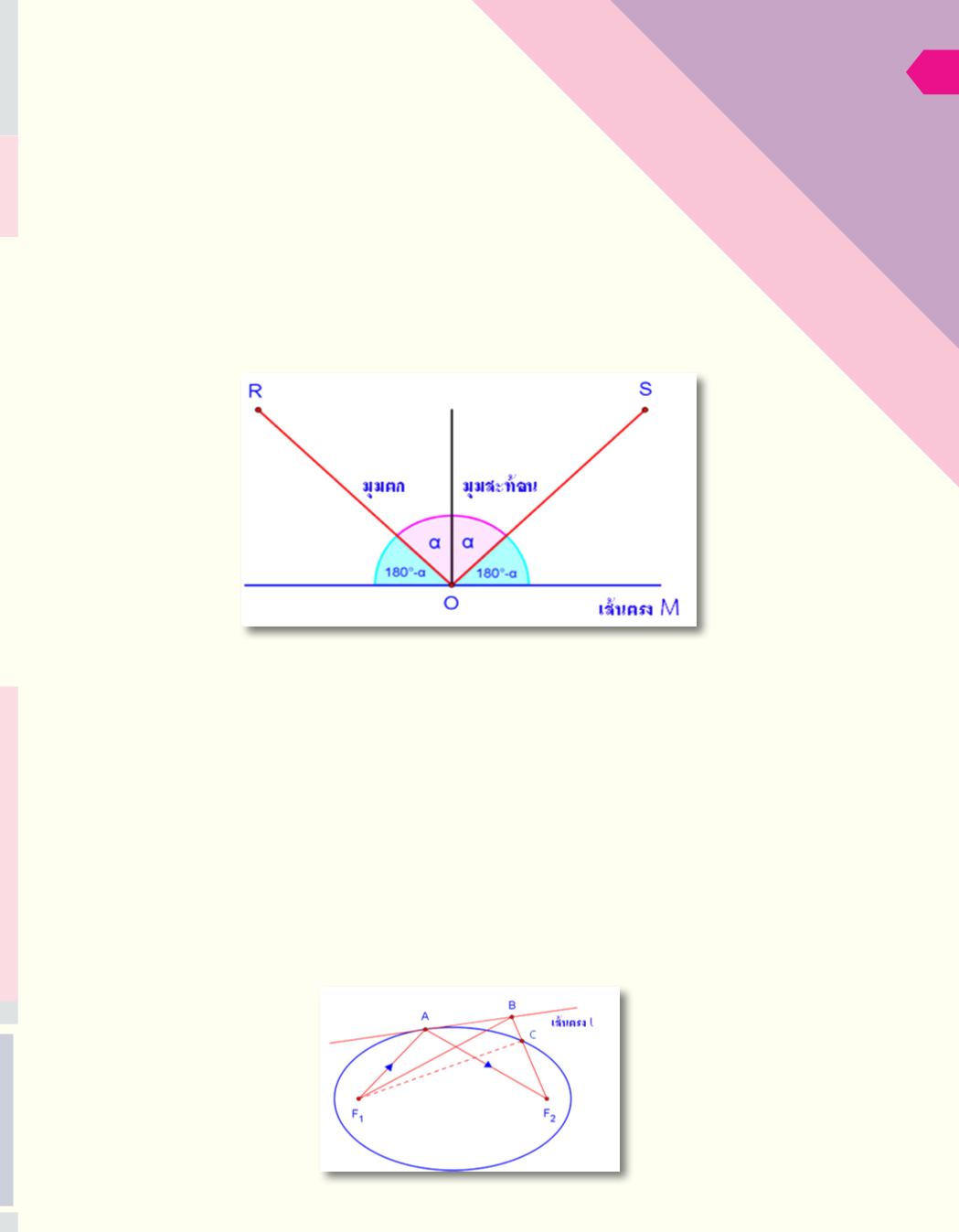
สมบัติดังกล่าวอธิบายได้โดยเริ่มจากกฎการสะท้อนของแสง
บนเส้นตรง เพราะเมื่อแสงเดินทางไปกระทบกับเส้นตรงแล้ว
แสงจะถูกสะท้อนออกมาโดยมุมตกกระทบเท่ากับมุมสะท้อน
ดังรูปที่ 3 ท�
ำให้แสดงได้ด้วยว่าระยะทางของแสงที่เดินทางจาก
จุด R ไปกระทบจุด O แล้วสะท้อนไปยังจุด S เป็นระยะทาง
ที่สั้นที่สุด เมื่อเทียบกับระยะทางที่แสงเดินทางจากจุด R
ไปกระทบจุดอื่น ๆ บนเส้นตรง M แล้วสะท้อนไปยังจุด S
(อ่านวิธีการพิสูจน์ได้จากหนังสือเพิ่มเติมเสริมศักยภาพการ
เรียนรู้คณิตศาสตร์มัธยมศึกษาตอนปลาย (ม.4-6) : เรขาคณิตวิเคราะห์)
จากรูปที่ 2 ถ้าจะแสดงว่าแสงเดินทางจากจุด F
1
ไปกระทบกับ
พื้นผิวทรงรีที่จุด P แล้วสะท้อนไปยังจุด F
2
ก็เพียงแค่แสดงว่า
ระยะทางของแสงที่เดินทางจากจุด F
1
ไปกระทบผิวทรงรีที่จุด P
แล้วสะท้อนไปยังจุด F
2
เป็นระยะทางที่สั้นที่สุดเมื่อเทียบกับ
ระยะทางที่แสงเดินทางจากจุด F
1
ไปกระทบจุดอื่น ๆ บนเส้น
สัมผัสวงรีที่จุด P แล้วสะท้อนไปยังจุด F
2
ซึ่งสามารถพิสูจน์ได้
ดังนี้
รูปที่ 3 การสะท้อนของแสงบนเส้นตรง
การพิสูจน์
จากรูปที่ 4 ให้ A เป็นจุดใด ๆ บนวงรี สร้างเส้นตรง l ซึ่งเป็นเส้นสัมผัสของวงรีที่จุด A
ให้ B เป็นจุดใด ๆ บนเส้นตรง l โดยที่จุด B ไม่ทับจุด A
ให้ C เป็นจุดตัดของวงรีกับเส้นตรง BF
2
จากบทนิยามของวงรี จะได้ว่า
F
1
C + CF
2
= F
1
A + AF
2
จากอสมการอิงรูปสามเหลี่ยม (triangle inequality) จะได้ว่า
F
1
B + BC > F
1
C
ดังนั้น F
1
B + BF
2
= F
1
B + BC + CF
2
> F
1
C + CF
2
= F
1
A + AF
2
จะได้ว่าจุด A เป็นจุดบนเส้นตรง l ที่ท�
ำให้ระยะทางของแสงที่เดินทางจาก F
1
ไปตกกระทบเส้นตรง l แล้วสะท้อนไปยัง
F
2
เป็นระยะทางที่สั้นที่สุด จากหลักการสะท้อนแสงบนเส้นตรงที่ได้กล่าวมา จะได้ว่ามุมตกกระทบเท่ากับมุมสะท้อน ดังนั้นแสงที่เดิน
ทางจากโฟกัสหนึ่งของทรงรีไปกระทบกับพื้นผิวของทรงรีจะถูกสะท้อนไปยังอีกโฟกัสหนึ่งของทรงรีเสมอ
รูปที่ 4
















