
24
นิตยสาร สสวท
การน�
ำจ�
ำนวนเชิงซ้อนไปใช้ไขปัญหาขุมทรัพย์นี้ จะต้องท�
ำความเข้าใจความหมายของการคูณ
จ�
ำนวนเชิงซ้อนก่อน จากที่เคยเรียนมาแล้วว่า การคูณจ�
ำนวนเชิงซ้อนด้วยจ�
ำนวนจริงเปรียบได้กับการคูณเวกเตอร์
ด้วยปริมาณสเกลาร์ ตัวอย่างเช่น เมื่อน�
ำจ�
ำนวนจริง 3 ไปคูณจ�
ำนวนเชิงซ้อน 2+3i จะได้ 6+9i หรือกล่าวว่า
ผลคูณจะเป็น 3 เท่าของจ�
ำนวนเชิงซ้อน 2+3i ดังรูปที่ 2 หรือเขียนในรูปเวกเตอร์ ได้เป็น
3
(1
1
2
2
3
= 6
9 -— 1
2—
(0,0)
(2,3)
0 1
1
2
3
4
2
-2 -1
-1
M ²
+
Q(-1,0)
90°
ll
ll
M ²
Q(-1,0)
90°
-1-b+(1+a)i
-(1+a)-bi
(-1-a,-b)
-b+(1+a)i
-b,(1+a)
(-1-b,1+a)
+
ซึ่งก็จะได้ผลคูณเป็นเวกเตอร์ที่มีทิศทางเดิมแต่มีขนาดเป็น 3 เท่า ในท�
ำนองเดียวกัน หากน�
ำจ�
ำนวนจริงลบ เช่น
0 1
2
3
4
5
6 7
3
(1+b)+(-1-b)
2
2
, (1-a)+(1+a)
1
2
2
3
= 6
9 -— 1
2—
(0,0)
(2,3)
0 1
1
2
3
4
2
-2 -1
-1
3
(0,0)
(2,3)
Y
M ²
M ¹
X
+
+
P(1,0)
R(a,b)
90°
Q(-1,0)
90°
-1
1
i
-i
0
0
(6,9)
1
2
3
4
5
6
7
8
9
10
-2 -1
-1
90°
ll
ll
l
l
Y
M ²
M ¹
X
P
R
90°
Q
i
-1
0
1
1
-2
2
90°
Y
M ²
X
P(1,0)
R(a,b)
Q(-1,0)
90°
-1-b+(1+a)i
-(1+a)-bi
(-1-a,-b)
-b+(1+a)i
-b,(1+a)
(-1-b,1+a)
Y
M ¹
X
+
P(1,0)
b+(1-a)i
b,(1-a)
1+b+(1-a)i
(1-a)-bi
(1-a,-b)
(1+b,1-a)
R(a,b)
Q(-1,0)
90°
90°
+
90°
+
+
-(1+b)+(1+a)i
(1+b)+(1-a)i
ไปคูณจะได้ผลคูณเป็นเวกเตอร์ที่มีทิศทางตรงกันข้ามแต่มีขนาดเป็น
0 1
2
3
4
5
6 7
3
(1+b)+(-1-b)
2
2
, (1-a)+(1+a)
1
2
2
3
= 6
9 -— 1
2—
(0,0)
(2,3)
0 1
1
2
3
4
2
-2 -1
-1
3
(0,0)
(2,3)
Y
M ²
M ¹
X
+
+
P(1,0)
R(a,b)
90°
Q(-1,0)
-1
(6,9)
1
2
3
4
5
6
7
8
9
10
-2 -1
-1
90°
ll
ll
l
l
M ²
Q
-1
-2
90°
Y
M ²
X
P(1,0)
R(a,b)
Q(-1,0)
90°
-1-b+(1+a)i
-(1+a)-bi
(-1-a,-b)
-b+(1+a)i
-b,(1+a)
(-1-b,1+a)
Q(-1,0)
+
90°
+
-(1+b)+(1+a)i
เท่า
0 1
2
3
4
5
6 7
2
2
(0,0)
(2,3)
0 1
1
2
3
4
2
-2 -1
-1
3
(0,0)
(2,3)
Y
M ²
M ¹
X
+
+
P(1,0)
R(a,b)
90°
Q(-1,0)
(6,9)
1
2
3
4
5
6
7
8
9
10
-2 -1
-1
90°
ll
ll
l
l
Y
M ²
-b,(1+a)
(-1-b,1+a)
Q(-1,0)
+
รูปที่ 2
การคูณ 2+3i ด้วย 3
ลองพิจารณาการคูณจ�
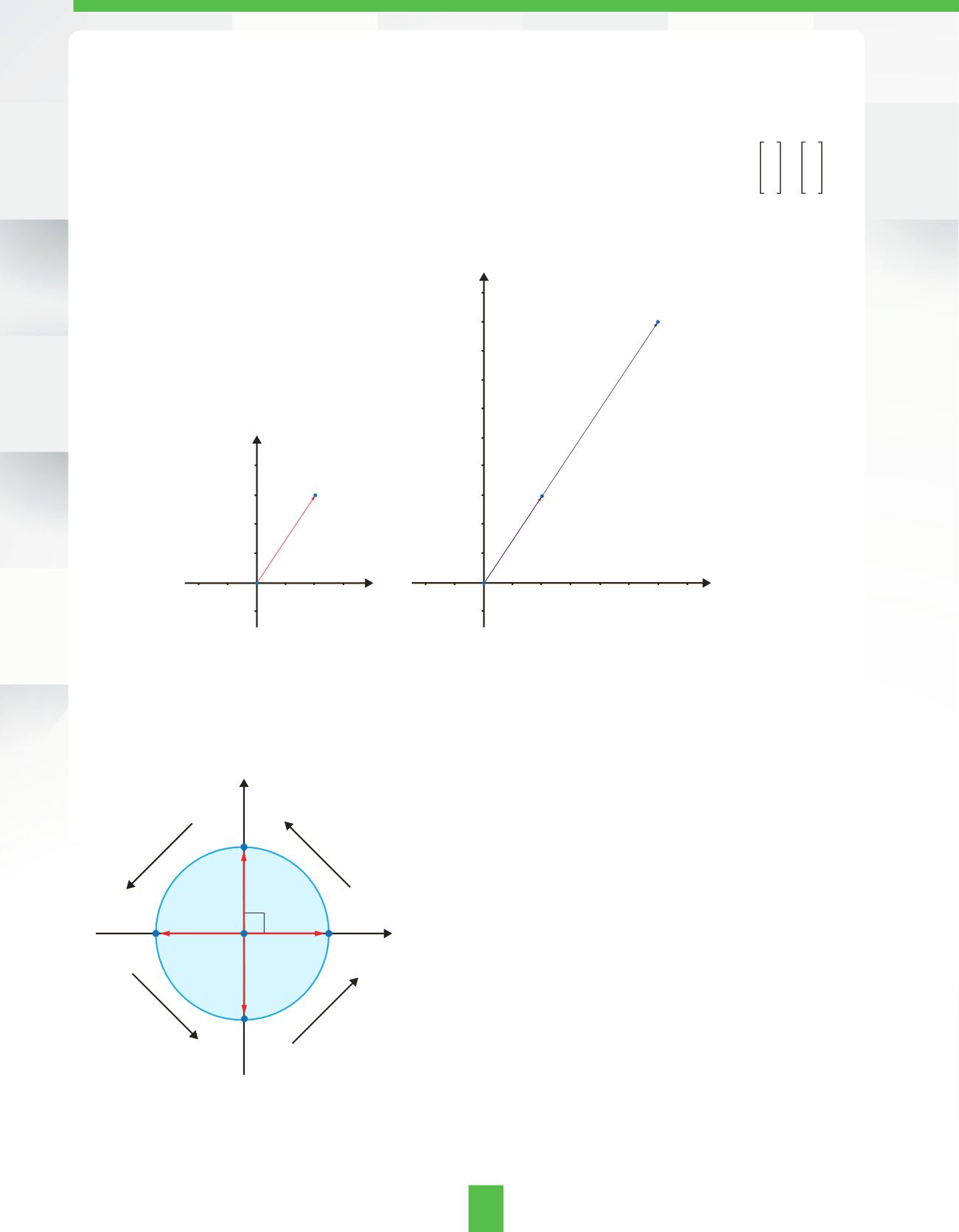
ำนวนเชิงซ้อนด้วย i เมื่อคูณ 1 ด้วย i จะได้ i และเมื่อคูณผลคูณด้วย i ไปเรื่อยๆ
จะได้ –1, –i และ 1 ตามล�
ำดับ สามารถเขียนแสดงในรูปเวกเตอร์ได้ดังรูปที่ 3
90°
-1
1
i
-i
0
0
รูปที่ 3
การคูณ 1 ด้วย i
การคูณจ�
ำนวนเชิงซ้อนด้วย i เป็นการหมุนเวกเตอร์
รอบจุด (0,0) เป็นมุม 90 องศา ในทิศทวนเข็มนาฬิกา
ในท�
ำนองเดียวกัน การคูณจ�
ำนวนเชิงซ้อนด้วย –i เป็นการหมุน
เวกเตอร์รอบจุด (0,0) ไปเป็นมุม 90 องศา ในทิศตามเข็มนาฬิกา
เ มื่ อ น�
ำ ล า ย แ ท ง ขุ ม ท รั พ ย์ ม า เ ขี ย น ล ง บ น
ระนาบเชิงซ้อน ดังรูปที่ 4 โดยก�
ำหนดจุด R(a,b) แทน
ต�
ำแหน่งของที่แขวนคอนักโทษ จุด P และ Q แทน ต�
ำแหน่ง
ต้นสนและต้นโอ๊ก ตามล�
ำดับ ให้แกนจริงเป็นเส้นตรงที่ผ่าน
ต้นไม้ทั้งสองต้น และแกนจินตภาพเป็นเส้นตรงที่ตั้งฉากกับ
แกนจริงและตัดแกนจริงที่จุดกึ่งกลางระหว่างต้นไม้ทั้งสอง
โดยไม่เสียนัยทั่วไป เราสามารถก�
ำหนดให้ P มีพิกัดเป็น (1,0)
และ Q มีพิกัดเป็น (–1,0)


















