
25
ปีที่ 44 ฉบับที่ 198 มกราคม-กุมภาพันธ์ 2559
Y
M ²
M ¹
X
+
+
P(1,0)
R(a,b)
90°
Q(-1,0)
90°
ll
ll
l
l
M ²
-2
Y
M ²
X
P(1,0)
R(a,b)
Q(-1,0)
90°
-1-b+(1+a)i
-(1+a)-bi
(-1-a,-b)
-b+(1+a)i
-b,(1+a)
(-1-b,1+a)
Q(-1
+
90°
+
-(1+b)+(1+a
90°
-1
1
-i
0
0
Y
M ²
M ¹
X
P
R
90°
Q
i
-1
0
1
1
-2
2
90°
Y
M ¹
X
+
P(1,0)
b+(1-a)i
b,(1-a)
1+b+(1-a)i
(1-a)-bi
(1-a,-b)
(1+b,1-a)
R(a,b)
Q(-1,0)
90°
90°
+
+
-(1+b)+(1+a)i
(1+b)+(1-a)i
จะสังเกตเห็นว่า เวกเตอร์ RP ที่เกิดจากการเดิน
จากที่แขวนคอนักโทษไปยังต้นสน สามารถมองได้เป็น
จ�
ำนวนเชิงซ้อน (1–a)–bi การหันไปทางซ้ายเป็นมุมฉาก
เปรียบได้กับการคูณ (1–a)–bi ด้วย i ซึ่งได้เป็น b+(1–a)i
ดังนั้น จากรูปที่ 5 จะได้ว่า พิกัดของจุด M1 คือ (1+b,1–a)
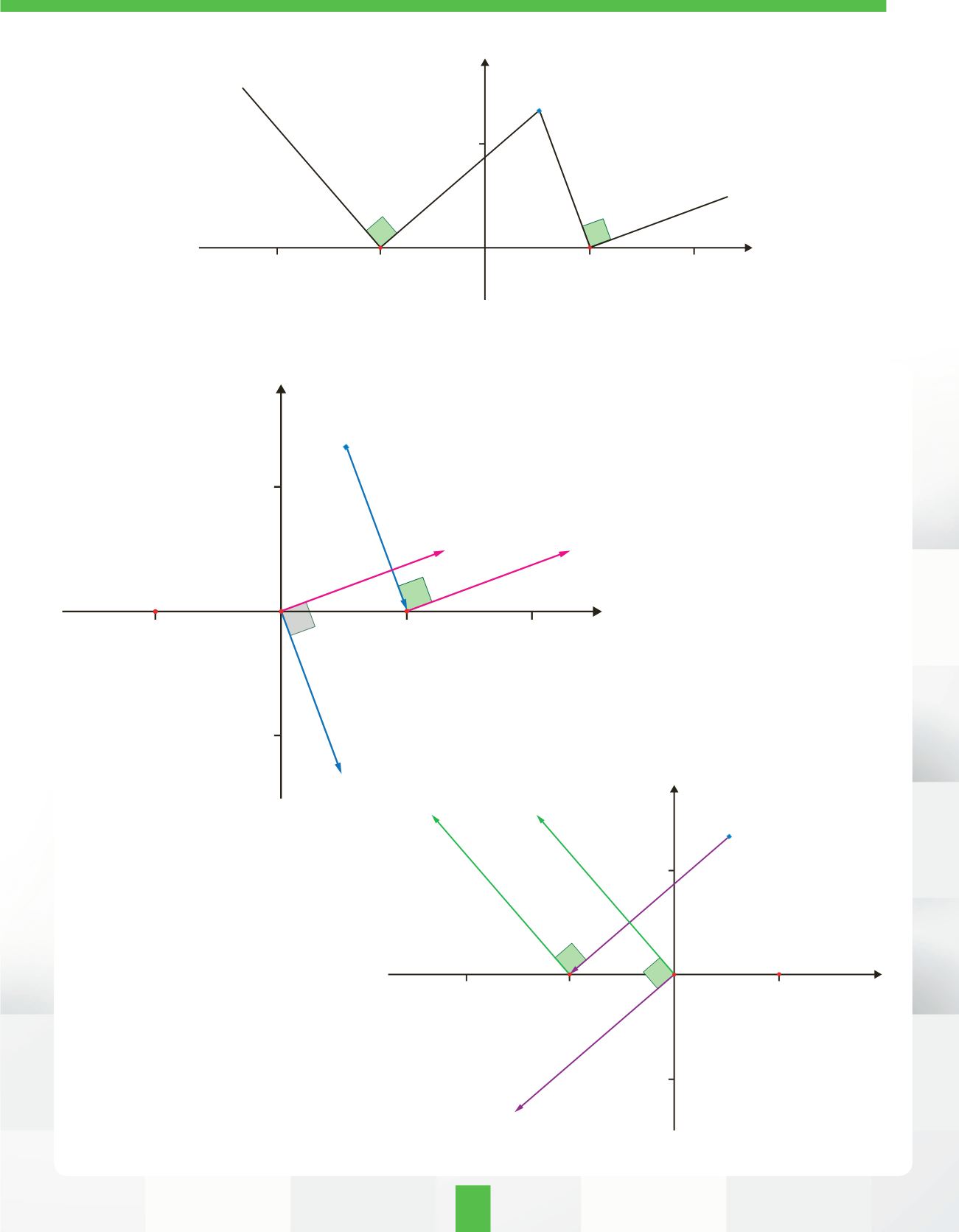
รูปที่ 4
ลายแทงขุมทรัพย์บนระนาบเชิงซ้อน
ในท�
ำนองเดียวกัน จะได้พิกัดของจุด M
2
คือ
(–1–b,1+a) ดังแสดงในรูปที่ 6
0 1
2
3
4
5
6
(0,0)
(2,3)
0 1
1
2
3
4
2
-2 -1
-1
3
(0,0)
(2,3)
Y
M ²
M ¹
+
+
P(1,0)
R(a,b)
90°
Q(-1,0)
1
2
3
4
5
6
7
8
9
-2 -1
-1
90°
ll
ll
l
l
Y
M ²
X
P(1,0)
R(a,b)
Q(-1,0)
90°
-1-b+(1+a)i
-(1+a)-bi
(-1-a,-b)
-b+(1+a)i
-b,(1+a)
(-1-b,1+a)
+
90°
รูปที่ 5
การค�
ำนวณหาพิกัดของจุด M
1
รูปที่ 6
การค�
ำนวณหาพิกัดของจุด M
2


















