
26
นิตยสาร สสวท
ดังนั้น จุดที่ฝังขุมทรัพย์ หรือจุดกึ่งกลางระหว่างจุด M
1
และ M
2
คือ
ซึ่งเท่ากับ (0,1) หรือ i ดังแสดงในรูปที่ 7
0 1
2
3
4
5
6 7
3
(1+b)+(-1-b)
2
2
, (1-a)+(1+a)
1
2
2
3
= 6
9 -— 1
2—
(0,0)
(2,3)
0 1
1
2
3
4
2
-2 -1
-1
3
(0,0)
(2,3)
Y
M ²
M ¹
X
+
+
P(1,0)
R(a,b)
90°
Q(-1,0)
90°
-1
1
i
-i
0
0
(6,9)
1
2
3
4
5
6
7
8
9
10
-2 -1
-1
90°
ll
ll
l
l
Y
M ²
M ¹
X
P
R
90°
Q
i
-1
0
1
1
-2
2
90°
Y
M ²
X
P(1,0)
R(a,b)
Q(-1,0)
90°
-1-b+(1+a)i
-(1+a)-bi(-1-a,-b)
-b+(1+a)i
-b,(1+a)
(-1-b,1+a)
Y
M ¹
X
+
P(1,0)
b+(1-a)i
b,(1-a)
1+b+(1-a)i
(1-a)-bi
(1-a,-b)
(1+b,1-a)
R(a,b)
Q(-1,0)
90°
90°
+
90°
+
+
-(1+b)+(1+a)i(1+b)+(1-a)i
Y
M ²
M ¹
X
P
R
90°
Q
i
-1
0
1
1
-2
2
90°
(1-a,-b)
+
+
-(1+b)+(1+a)i
(1+b)+(1-a)i
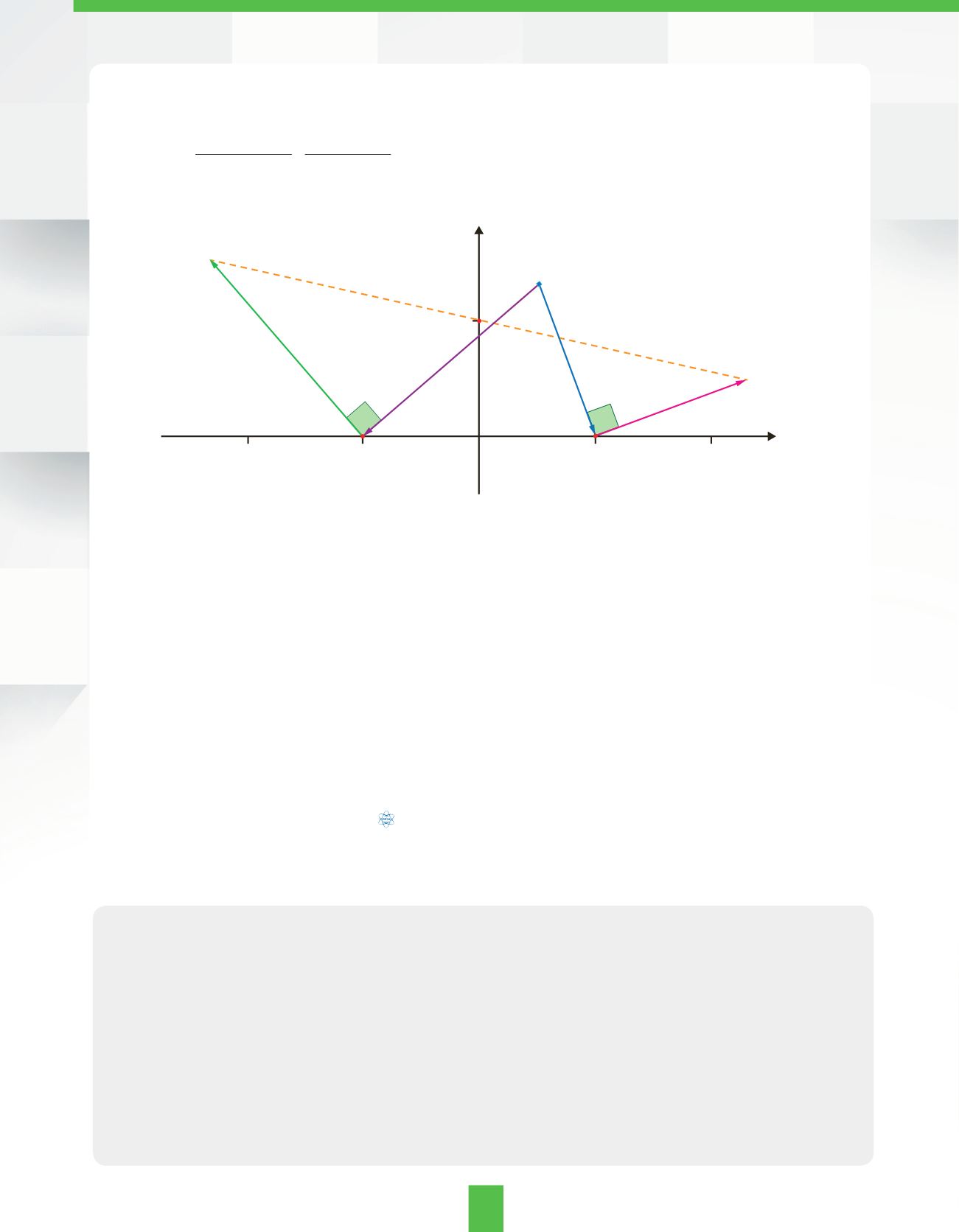
รูปที่ 7
การค�
ำนวณหาพิกัดของจุดที่ฝังขุมทรัพย์
จากรูป จะเห็นว่าจุดที่ฝังขุมทรัพย์มีพิกัดเป็น (0,1) ซึ่งก็คือ จุดที่ห่างจากจุดกึ่งกลางของต้นไม้ทั้งสองต้น
ไปทางเหนือ โดยจุดที่ฝังขุมทรัพย์มีระยะห่างจากจุดกึ่งกลางเท่ากับระยะทางจากจุดกึ่งกลางไปยังต้นไม้ต้นใดต้นหนึ่ง
จะสังเกตเห็นว่า พิกัดที่ได้ไม่ขึ้นกับ a และ b เลย นั่นแสดงว่า ต�
ำแหน่งของจุดที่ฝังขุมทรัพย์ สามารถหาได้จาก
ต�
ำแหน่งของต้นโอ๊กและต้นสน โดยไม่จ�
ำเป็นต้องรู้ต�
ำแหน่งที่แขวนคอนักโทษ
การคูณจ�
ำนวนเชิงซ้อนด้วย i และ –i ดังที่กล่าวข้างต้น เปรียบได้กับการหมุนเวกเตอร์บนระนาบสองมิติ
ท�
ำให้สามารถแก้ปัญหาข้างต้นได้ง่ายขึ้น ผู้ที่สนใจวิธีคิดอย่างละเอียดสามารถศึกษาเพิ่มเติมได้จากสื่อวีดิทัศน์
ชุด “Math in My Life เพราะคณิตอยู่ในชีวิตจริง ”Season 2 ซึ่งจัดท�
ำโดย สาขาวิชาคณิตศาสตร์ สสวท. ติดตาม
ได้ทาง YouTube ช่อง IPST Thailand
บรรณานุกรม
Azad, Kalid.
A Visual, Intuitive Guide to Imaginary Numbers
. สืบค้นเมื่อ 30 พฤษภาคม 2558, จาก http://betterexplained.com/
articles/a-visual-intuitive-guide-to-imaginary-numbers/
Gamow, George. (1947).
One, Two, Three … Infinity: Acts and Speculations of Science
. NY: Dover Publications.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2553).
หนังสือเรียนรายวิชาเพิ่มเติม คณิตศาสตร์ เล่ม 3
ชั้นมัธยมศึกษาปีที่ 4-6 กลุ่มสาระการเรียนรู้คณิตศาสตร์ ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551
.
กรุงเทพมหานคร: โรงพิมพ์องค์การค้า สกสค.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2553).
หนังสือเรียนรายวิชาเพิ่มเติม คณิตศาสตร์ เล่ม 4
ชั้นมัธยมศึกษาปีที่ 4-6 กลุ่มสาระการเรียนรู้คณิตศาสตร์ ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551
.
กรุงเทพมหานคร: โรงพิมพ์องค์การค้า สกสค.


















