
35
ปีที่ 46 ฉบับที่ 214 กันยายน - ตุลาคม 2561
ความไม่สม�่ำเสมอของผู้ทดลอง (Experimenter’s Inconsistency) การลดความคลาดเคลื่อนแบบสุ่มสามารถท�ำได้โดยทดลอง
ซ�้ำครั้งมากขึ้น ส่วนความคลาดเคลื่อนเชิงระบบ จะเป็นการทดลองที่มีความแม่นต�่ำ (Low Accuracy) ซึ่งเกิดครั้งแล้วครั้งเล่า
ในสภาวะการทดลองเดียวกัน สาเหตุของความคลาดเคลื่อนเชิงระบบจะเกี่ยวข้องกับปัจจัยเฉพาะของการทดลอง เช่น
ข้อจ�ำกัดเกี่ยวกับอุปกรณ์การทดลอง ซึ่งส่วนใหญ่จะไม่สามารถพิจารณาหาได้ง่าย ดังนั้น การลดความคลาดเคลื่อนเชิงระบบ
จะเป็นไปในลักษณะการใช้เทคนิคทางการทดลองใหม่ หรือเครื่องมือวัดที่มีเทคโนโลยีก้าวหน้าขึ้น เพื่อให้สามารถหา
ค่าตัวแปรเดิมมาเปรียบเทียบให้มีความแม่นยิ่งขึ้น
การแสดงผลของปริมาณในการรายงานผลการทดลอง
ในยุคหนึ่ง การทดลองจะถูกจ�ำกัดโดยเทคโนโลยีหรือเครื่องวัดที่มีอยู่และหาได้ในขณะนั้น การลดความคลาดเคลื่อน
ของผลการทดลองหรือการสังเกต มักจะท�ำโดยการทดลองวัดค่าซ�้ำ เช่น ทดลองซ�้ำ 3 ครั้ง หรือ 3 Replicates ซึ่งอาจเป็น
การทดลองด้วยเครื่องมือเดิม (Technical Replicates) หรือในทางชีววิทยา ซึ่งเป็นการท�ำซ�้ำในสิ่งมีชีวิตชนิดเดิมแต่เป็นตัวใหม่
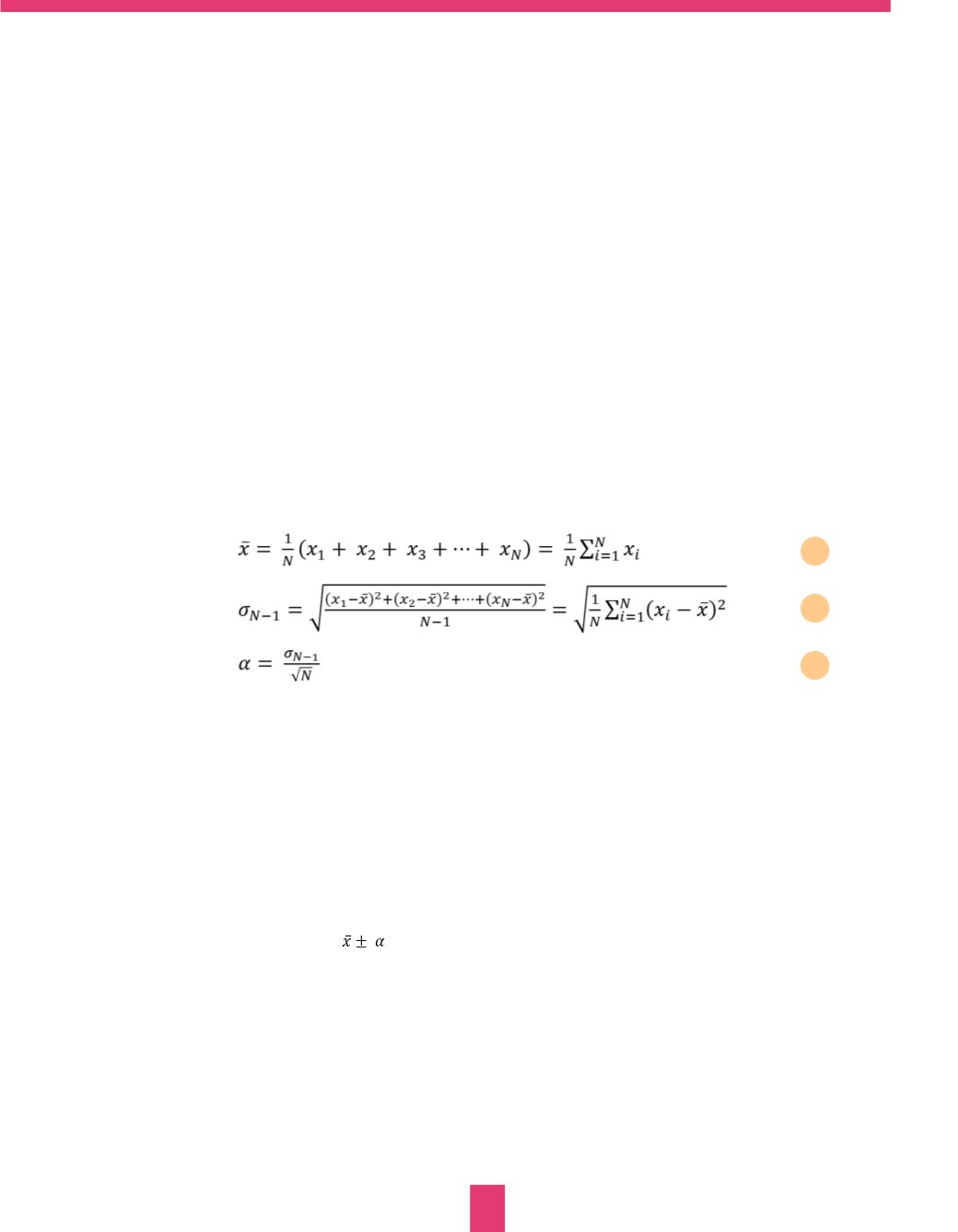
ที่เรียกว่า Biological Replicates การแสดงผลจากการวัดค่าซ�้ำจะต้องค�ำนึงถึงค่าเฉลี่ย (Means) จากการวัดหลายๆ ครั้ง และ
ความคลาดเคลื่อน (Error) จาการวัดค่าหลายๆ ครั้ง ซึ่งจะใช้เป็นส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation; SD) หรือ
ความคลาดเคลื่อนมาตรฐานของค่าเฉลี่ย (Standard Error of the Mean; SEM) ดังสมการที่ 1 ถึง 3 ตามล�ำดับ
1
2
3
หมายเหตุ
1. ในการทดลองจริงเราสามารถน�ำข้อมูลที่วัดได้ และใช้สูตรจากโปรแกรมวิเคราะห์ข้อมูล เช่น Microsoft Excel
เพื่อค�ำนวณหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐาน รวมถึงสร้างสูตรเพื่อหาค่าคลาดเคลื่อน
2. เหตุผลที่ใช้ส่วนเบี่ยงเบนมาตรฐาน เพราะเป็นการวัดความแตกต่างที่วัดในแต่ละครั้งจากค่าเฉลี่ยในลักษณะที่
ป้องกันการหักล้าง เนื่องจากความแตกต่างของค่าที่วัดแต่ละครั้งกับค่าเฉลี่ยมีเครื่องหมายตรงกันข้าม
ดังนั้น ปริมาณที่ได้จากการท�ำการทดลองวัดซ�้ำ ในกรณีที่ใช้ความคลาดเคลื่อนมาตรฐานของค่าเฉลี่ยเป็นค่า
ความคลาดเคลื่อนสามารถแสดงได้เป็น
นอกจากนี้ การแสดงปริมาณดังกล่าวยังต้องค�ำนึงถึงเลขนัยส�ำคัญ (Significant
Figures) ด้วย โดยทั่วไปเลขนัยส�ำคัญที่แสดงขึ้นกับความละเอียดของเครื่องมือที่ใช้ในการวัด ซึ่งอาจแตกต่างกันเมื่อใช้
เครื่องวัดที่เป็น Analog หรือเครื่องวัด Digital หรือความไม่แน่นอนของปริมาณที่เครื่องมือวัดวัดได้ ทั้งนี้ การรายงานผล
การวัดที่น่าเชื่อถือจะต้องก�ำหนดเลขทศนิยมของปริมาณที่วัดเฉลี่ย ให้สอดคล้องกับความไม่แน่นอนของเครื่องมือวัด
(ใช้จ�ำนวนทศนิยมเท่ากัน) แทนการรายงานเลขทศนิยมทุกต�ำแหน่งที่ค�ำนวณได้ ตัวอย่างเช่น ถ้าผลการค�ำนวณค่าเฉลี่ยของ
การวัดความกว้างของโต๊ะ 3 ครั้ง ด้วยไม้บรรทัด เป็น 25.42 cm ความไม่แน่นอนของการวัดด้วยไม้บรรทัดเท่ากับ 0.1 cm
และค่าความคลาดเคลื่อนที่ค�ำนวณได้เป็น 0.24 cm ควรรายงานค่าการวัดความกว้างของโต๊ะเป็น 25.4 ± 0.2 cm (รายงาน
ค่าความคลาดเคลื่อนที่มากที่สุดที่คิดว่าจะเป็นไปได้)


















